北京市21、22中联盟校2021-2022学年九年级上学期10月月考数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 下列方程中一元二次方程的个数为( )
①2x2-3=0; ②x2+y2=5; ③ ; ④
A、1个 B、2个 C、3个 D、4个2. 下列叙述正确的是( )A、形如的方程叫一元二次方程 B、方程不含有常数项 C、一元二次方程中,二次项系数、一次项系数及常数项均不能为0 D、是关于y的一元二次方程3. 如图,△ABC经过变换得到△AB'C',其中△ABC绕点A逆时针旋转60°的是( )A、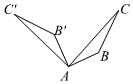 B、
B、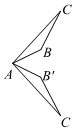 C、
C、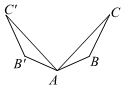 D、
D、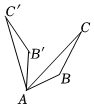 4. 抛物线y=(x﹣1)2+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,﹣3) D、(3,﹣1)5. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 老师给出了二次函数y=ax2+bx+c(a≠0)的部分对应值如表:
4. 抛物线y=(x﹣1)2+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,﹣3) D、(3,﹣1)5. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 老师给出了二次函数y=ax2+bx+c(a≠0)的部分对应值如表:x
…
﹣3
﹣2
0
1
3
5
…
y
…
7
0
﹣8
﹣9
﹣5
7
…
同学们讨论得出了下列结论,
①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当﹣2<x<4时,y<0;④当x>1时,y随x的增大而增大;⑤若方程ax2+bx+c=m有两个不相等的实数根,则m>﹣9.
其中正确的个数是( )
A、2个 B、3个 C、4个 D、5个7. 如图,在中, , 将绕点C逆时针旋转得到 , 点A,B的对应点分别为D,E,连接 . 当点A,D,E在同一条直线上时,下列结论一定正确的是( )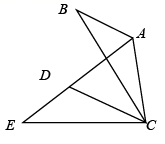 A、 B、 C、 D、8. 跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度(单位:)与水平距离(单位:)近似满足函数关系().下图记录了某运动员起跳后的与的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A、 B、 C、 D、8. 跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度(单位:)与水平距离(单位:)近似满足函数关系().下图记录了某运动员起跳后的与的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )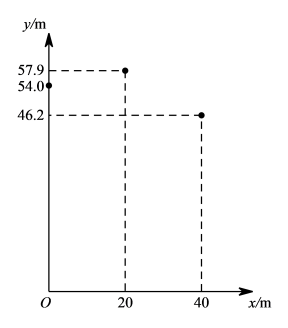 A、 B、 C、 D、9. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )
A、 B、 C、 D、9. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )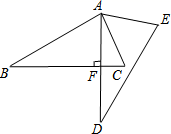 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 一元二次方程x2﹣4x+4=0的解是 .
11. 已知m是关于x的方程x2﹣3x﹣4=0的一个根,则3m2﹣9m﹣2= .12. 若二次函数y=2x2-3的图象上有两个点A(1,m),B(2,n),则mn(填“<”“=”或“>”).13. 如图,ABC的三个顶点都在方格纸的格点上,其中A点的坐标是 , 现将ABC绕A点按逆时针方向旋转 , 则旋转后点C对应点的坐标是 . 14. 如图,抛物线的对称轴为 , 点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为 .
14. 如图,抛物线的对称轴为 , 点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为 .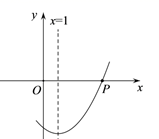 15. 已知抛物线y=ax2+bx+c的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b=0;③a﹣b+c<0;④b2>4ac;⑤当x<2时,y随x的增大而增大,你认为其中正确的是 .(填序号)
15. 已知抛物线y=ax2+bx+c的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b=0;③a﹣b+c<0;④b2>4ac;⑤当x<2时,y随x的增大而增大,你认为其中正确的是 .(填序号)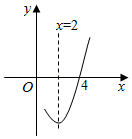 16. 定义:若抛物线与x轴有两个交点,且这两个交点与它的顶点所构成的三角形是直角三角形,则把这种抛物线称作“和美抛物线”.如图,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),… Bn(n,yn)(n为正整数)依次是直线y 上的点,这组抛物线与x轴正半轴的交点依次是A1(a1 , 0),A2(a2 , 0),A3(a3 , 0),…An+1(an+1 , 0)(0<a1<1,n为正整数).若这组抛物线中存在和美抛物线,则a1=.
16. 定义:若抛物线与x轴有两个交点,且这两个交点与它的顶点所构成的三角形是直角三角形,则把这种抛物线称作“和美抛物线”.如图,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),… Bn(n,yn)(n为正整数)依次是直线y 上的点,这组抛物线与x轴正半轴的交点依次是A1(a1 , 0),A2(a2 , 0),A3(a3 , 0),…An+1(an+1 , 0)(0<a1<1,n为正整数).若这组抛物线中存在和美抛物线,则a1=.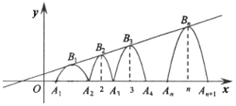
三、解答题
-
17. 解方程:(1)、(2)、6x2-x-2=0.18. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系, 的顶点均在格点上,点 的坐标为(1,0).
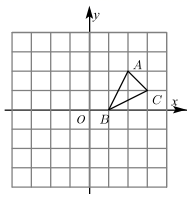 (1)、画出将 绕原点 按顺时针旋转90°所得的 ,并写出 点的坐标.(2)、求线段 的长度.19. 如图,在 中, .将 绕点 按逆时针方向旋转后得 ,连接 .当 时,求 的度数.
(1)、画出将 绕原点 按顺时针旋转90°所得的 ,并写出 点的坐标.(2)、求线段 的长度.19. 如图,在 中, .将 绕点 按逆时针方向旋转后得 ,连接 .当 时,求 的度数.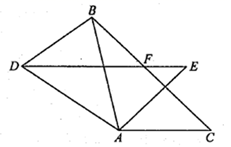 20. 已知抛物线C1:y=(x+2)2﹣1,抛物线C1 , 的顶点为A,与y轴的交点为B.
20. 已知抛物线C1:y=(x+2)2﹣1,抛物线C1 , 的顶点为A,与y轴的交点为B.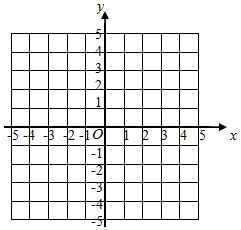
⑴点A的坐标是 ▲ , 点B的坐标是 ▲ ;
⑵在平面直角坐标系中画出C1的图象(不必列表);
⑶将抛物线C1向下平移3个单位,向右平移2个单位后得到抛物线C2 , 画出平移后的抛物线C2并写出抛物线C2的解析式.
21. 已知关于的方程有两个不相等的实数根.(1)、求的取值范围;(2)、若为满足条件的最大整数,求方程的根.22. 某商店销售一种进价为20元/双的手套,经调查发现,该种手套每天的销售量w(双)与销售单价x(元)满足w=﹣2x+80(20≤x≤40),设销售这种手套每天的利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?23. 有这样一个问题:探究函数y=(x﹣1)(x﹣2)(x﹣3)+x的性质.(1)、先从简单情况开始探究:①当函数y=(x﹣1)+x时,y随x增大而(填“增大”或“减小”);
②当函数y=(x﹣1)(x﹣2)+x时,它的图象与直线y=x的交点坐标为;
(2)、当函数y=(x﹣1)(x﹣2)(x﹣3)+x时,下表为其y与x的几组对应值.
x
…
﹣
0
1
2
3
4
…
y
…
﹣
﹣3
1
2
3
7
…
①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
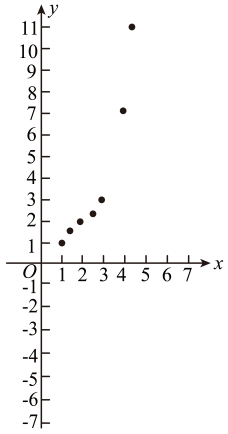
②根据画出的函数图象,写出该函数的一条性质: ▲ .
24. 随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.(1)、求2018年至2020年该省公共充电桩数量的年平均增长率;(2)、按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?25. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.26. 如图,抛物线与轴交于两点 , .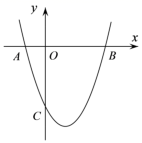 (1)、求 , 的值.(2)、观察函数的图象,直接写出当取何值时, .(3)、设抛物线交轴于点 , 在该抛物线的对称轴上是否存在点 , 使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.27. 在平面直角坐标系中,已知抛物线 , .
(1)、求 , 的值.(2)、观察函数的图象,直接写出当取何值时, .(3)、设抛物线交轴于点 , 在该抛物线的对称轴上是否存在点 , 使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.27. 在平面直角坐标系中,已知抛物线 , .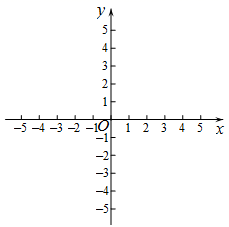 (1)、当时,①求抛物线G与x轴的交点坐标;
(1)、当时,①求抛物线G与x轴的交点坐标;②若抛物线G与线段只有一个交点,求n的取值范围;
(2)、若存在实数a,使得抛物线G与线段有两个交点,结合图象,直接写出n的取值范围.28. 定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1 , x2(x1<x2),分别以x1 , x2为横坐标和纵坐标得到点M(x1 , x2),则称点M为该一元二次方程的衍生点.(1)、若方程为x2﹣2x=0,写出该方程的衍生点M的坐标.(2)、若关于x的一元二次方程x2﹣(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.(3)、是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx﹣2(k﹣2)的图象上,若有请直接写出b,c的值,若没有说明理由.