安徽省淮南市西部地区2021-2022学年九年级上学期第三次调研数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 下列事件中是不可能事件的是( )A、任意写一个一元二次方程,有两个根 B、抛物线y=2x2+3x可由抛物线y=﹣2x2平移得到 C、圆外一点引圆的两条切线,它们的切线长相等 D、平分弦的直径垂直于弦2. 将分别标有“学”“习”“强”“国”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其它差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸的球上的汉字组成“强国”的概率是( )A、 B、 C、 D、3. 如图,△ABP是由△ACE绕A点旋转得到的,若∠BAP=40°,∠B=30°,∠PAC=20°,则∠E、∠BAE的度数分别为( )
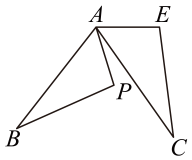 A、110°、100° B、120°、110° C、100°、110° D、120°、110°4. 如图,点O是▱ABCD的对称中心,l是过点O的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小是( )
A、110°、100° B、120°、110° C、100°、110° D、120°、110°4. 如图,点O是▱ABCD的对称中心,l是过点O的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小是( ) A、甲大 B、乙大 C、一样大 D、无法确定5. 如果抛物线 的顶点到 轴的距离是3,那么 的值等于( )A、8 B、14 C、8或14 D、-8或-146. 从1,2,3,4中任取两个不同的数,分别记为 和 ,则 的概率是( )A、 B、 C、 D、7. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<88. 圆内接正方形的面积为a,则圆的面积为( )A、 B、2πa C、 D、πa29. 如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以构成一个矩形,从这些矩形中任选一个,则所选矩形含点P的概率是( )
A、甲大 B、乙大 C、一样大 D、无法确定5. 如果抛物线 的顶点到 轴的距离是3,那么 的值等于( )A、8 B、14 C、8或14 D、-8或-146. 从1,2,3,4中任取两个不同的数,分别记为 和 ,则 的概率是( )A、 B、 C、 D、7. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<88. 圆内接正方形的面积为a,则圆的面积为( )A、 B、2πa C、 D、πa29. 如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以构成一个矩形,从这些矩形中任选一个,则所选矩形含点P的概率是( ) A、 B、 C、 D、10. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),为了了解该图案的面积是多少,我们采取了以下办法:用一个长为a,宽为b的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),现将若干次有效实验的结果绘制成了如图②所示的折线统计图,由此估计不规则图案的面积大约是( )
A、 B、 C、 D、10. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),为了了解该图案的面积是多少,我们采取了以下办法:用一个长为a,宽为b的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),现将若干次有效实验的结果绘制成了如图②所示的折线统计图,由此估计不规则图案的面积大约是( )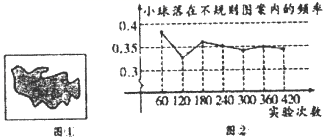 A、a2 B、ab C、b2 D、ab
A、a2 B、ab C、b2 D、ab二、填空题
-
11. 抛物线y=mx2+2mx﹣1的对称轴是 .12. △ABC绕着A点旋转后得到△A'B'C',若∠BAC'=130°,∠BAC=80°,则旋转角等于 .13. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是.
 14. 某水果公司以2.2元/千克的成本价购进10000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如表:
14. 某水果公司以2.2元/千克的成本价购进10000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如表:抽取的苹果总质量
100
200
300
400
500
1000
损坏苹果质量
10.60
19.42
30.63
39.24
49.54
101.10
苹果损坏的频率
0.106
0.097
0.102
0.098
0.099
0.101
①估计这批苹果损坏的概率为(精确到0.1);
②据此,若公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应定为元/千克.
三、解答题
-
15. 如图,已知⊙O的两条弦AB、CD,且AB=CD.求证:AD=BC.
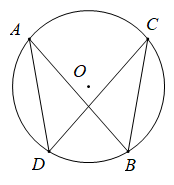 16. 求抛物线y=x2﹣x+1在﹣2≤x≤2的最大值与最小值.17. 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
16. 求抛物线y=x2﹣x+1在﹣2≤x≤2的最大值与最小值.17. 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P. (1)、PA与PB的数量关系是;(2)、若AB=12,求圆环的面积.18. 如图,在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点.
(1)、PA与PB的数量关系是;(2)、若AB=12,求圆环的面积.18. 如图,在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点.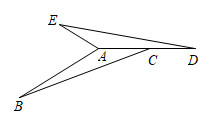 (1)、指出旋转中心,并求出旋转角的度数;(2)、求出∠BAE的度数和AE的长.19. 高新开发区某企业2020年1月份的产值达500万元,第一季度总产值为1820万元,问:2,3月份平均每月的增长率是多少?20. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
(1)、指出旋转中心,并求出旋转角的度数;(2)、求出∠BAE的度数和AE的长.19. 高新开发区某企业2020年1月份的产值达500万元,第一季度总产值为1820万元,问:2,3月份平均每月的增长率是多少?20. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD. (1)、求证:AC=BD;(2)、若图中阴影部分的面积是πcm2 , OA=2cm,求OC的长.21. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)、求证:AC=BD;(2)、若图中阴影部分的面积是πcm2 , OA=2cm,求OC的长.21. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.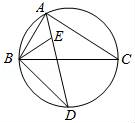 (1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.22. 阅读对话,解答问题:
(1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.22. 阅读对话,解答问题: (1)、分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;(2)、求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.23. 对于二次函数y=x2﹣4x+3和一次函数y=﹣x+1,我们把y=t(x2﹣4x+3)+(1﹣t)(﹣x+1)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线M.现有点A(1,0)和抛物线M上的点B(2,n),请完成下列任务:
(1)、分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;(2)、求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.23. 对于二次函数y=x2﹣4x+3和一次函数y=﹣x+1,我们把y=t(x2﹣4x+3)+(1﹣t)(﹣x+1)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线M.现有点A(1,0)和抛物线M上的点B(2,n),请完成下列任务:(尝试)
(1)、当t=2时,抛物线y=t(x2﹣4x+3)+(1﹣t)(﹣x+1)的顶点坐标为 .(2)、判断点A是否在抛物线M上;(3)、求n的值.(4)、通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线M总过定点,定点的坐标为 .(5)、二次函数y=﹣3x2+8x﹣5是二次函数y=x2﹣4x+3和一次函数y=﹣x+1的一个“再生二次函数”吗?如果是,求出t的值:如果不是,说明理由.