安徽省亳州市2021-2022学年九年级上学期12月月考数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 下列函数图象是双曲线的是( )A、y=x2+3 B、y=﹣x﹣5 C、y=﹣ D、y=﹣2. 二次函数的图象的顶点坐标是( )A、(3,-1) B、(-3,1) C、(-3,-1) D、(3,1)3. 如图,在△ABC中,∠C=90°,BC=1,AB= , 则下列三角函数值正确的是( )
 A、sinA= B、tanA=2 C、cosB=2 D、sinB=4. 如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A、sinA= B、tanA=2 C、cosB=2 D、sinB=4. 如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )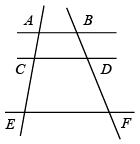 A、 B、 C、 D、15. 将二次函数y=(x﹣3)(x+2)的图象向左平移3个单位长度,平移后的函数表达式为( )A、y=x(x+5) B、y=(x+3)(x﹣2) C、y=x(x﹣1) D、y=(x﹣3)(x﹣5)6. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,关于x的一元二次方程ax2+bx+c=0的解分别为x1 , x2 , 则x1+x2的值为( )
A、 B、 C、 D、15. 将二次函数y=(x﹣3)(x+2)的图象向左平移3个单位长度,平移后的函数表达式为( )A、y=x(x+5) B、y=(x+3)(x﹣2) C、y=x(x﹣1) D、y=(x﹣3)(x﹣5)6. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,关于x的一元二次方程ax2+bx+c=0的解分别为x1 , x2 , 则x1+x2的值为( ) A、2 B、1 C、﹣1 D、﹣27. 如图要测量小河两岸相对的两点P,A的距离,点P位于点A正北方向,点C位于点A的北偏西46°,若测得PC=50米,则小河宽PA为( )
A、2 B、1 C、﹣1 D、﹣27. 如图要测量小河两岸相对的两点P,A的距离,点P位于点A正北方向,点C位于点A的北偏西46°,若测得PC=50米,则小河宽PA为( )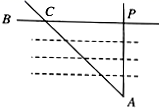 A、50sin44°米 B、50cos44° C、50tan44°米 D、50tan46°米8. 某商品的利润y(元)与售价x(元)之间的函数关系式为y=﹣x2+8x+9,且售价x的范围是1≤x≤3,则最大利润是( )A、16元 B、21元 C、24元 D、25元9. 如图,在等边三角形ABC中,AB=4,点E,F分别在AC,BC上,AE=CF=1,则BP•BE的值为( )
A、50sin44°米 B、50cos44° C、50tan44°米 D、50tan46°米8. 某商品的利润y(元)与售价x(元)之间的函数关系式为y=﹣x2+8x+9,且售价x的范围是1≤x≤3,则最大利润是( )A、16元 B、21元 C、24元 D、25元9. 如图,在等边三角形ABC中,AB=4,点E,F分别在AC,BC上,AE=CF=1,则BP•BE的值为( )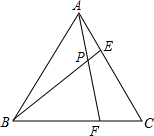 A、12 B、10 C、8 D、610. 在四边形ABCD中,∠A=45°,∠D=90°,AD∥BC,BC=1,CD=3.点P,Q同时从点A出发,点P以个单位长度/秒向点B运动,到达点B停止运动;点Q以2个单位长度/秒沿着AD→DC向点C运动,到达点C停止运动.设点Q运动时间为ts,△APQ的面积为S,则S随t变化的函数图象大致为( )
A、12 B、10 C、8 D、610. 在四边形ABCD中,∠A=45°,∠D=90°,AD∥BC,BC=1,CD=3.点P,Q同时从点A出发,点P以个单位长度/秒向点B运动,到达点B停止运动;点Q以2个单位长度/秒沿着AD→DC向点C运动,到达点C停止运动.设点Q运动时间为ts,△APQ的面积为S,则S随t变化的函数图象大致为( )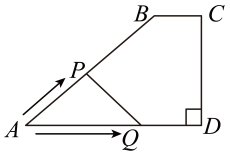 A、
A、 B、
B、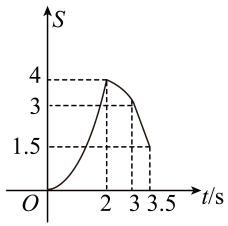 C、
C、 D、
D、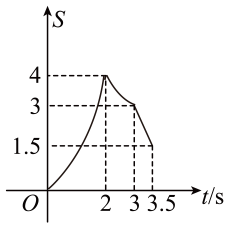
二、填空题
-
11. 如果a:b=3:2,且b是a和c的比例中项,那么b:c= .12. 已知点C是线段AB的黄金分割点(靠近A),AB=2,则BC= .13. 如图,将一副三板按图所示放置,∠DAE=∠ABC=90°,∠D=45°,∠C=30°,点E在AC上,过点A作AF∥BC交DE于点F,则= .
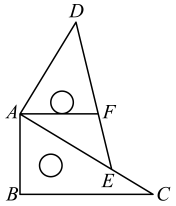 14. 二次函数y=x2﹣bx﹣1的顶点位置随着字母b的值变化而变化,顶点运动轨迹呈某种函数图象,该种函数即为原函数的模型函数.(1)、二次函数y=x2﹣bx﹣1的顶点坐标为 ;(用字母b表示)(2)、若某二次函数与二次函数y=x2﹣bx﹣1的形状相同,其模型函数与二次函数y=x2﹣bx﹣1的模型函数关于x轴对称,且经过点(1,2),则该二次函数的表达式为 .
14. 二次函数y=x2﹣bx﹣1的顶点位置随着字母b的值变化而变化,顶点运动轨迹呈某种函数图象,该种函数即为原函数的模型函数.(1)、二次函数y=x2﹣bx﹣1的顶点坐标为 ;(用字母b表示)(2)、若某二次函数与二次函数y=x2﹣bx﹣1的形状相同,其模型函数与二次函数y=x2﹣bx﹣1的模型函数关于x轴对称,且经过点(1,2),则该二次函数的表达式为 .三、解答题
-
15. 求值:16. 已知抛物线过点A(-1,0),B(0,6),对称轴为直线x=1, 求该抛物线的解析式.17. 如图,△ABC的顶点都在网格点上,点M的坐标为(0,1).
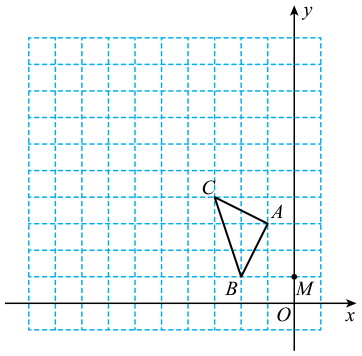 (1)、以点M为位似中心,把△ABC按3:1放大,在第二象限得到△A1B1C1 , 画出△A1B1C1;(2)、若△ABC的周长为m,面积为n,则上述所画的△A1B1C1的周长为 , 面积为 .18. 如图,在 中,点 、 分别在边 , 上, ,线段 分别交线段 , 于点 , ,且 .
(1)、以点M为位似中心,把△ABC按3:1放大,在第二象限得到△A1B1C1 , 画出△A1B1C1;(2)、若△ABC的周长为m,面积为n,则上述所画的△A1B1C1的周长为 , 面积为 .18. 如图,在 中,点 、 分别在边 , 上, ,线段 分别交线段 , 于点 , ,且 .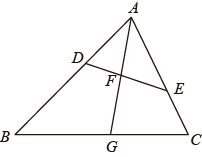 (1)、求证: ;(2)、若 ,求 的值.19. 如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2 .
(1)、求证: ;(2)、若 ,求 的值.19. 如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2 .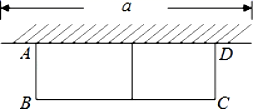 (1)、求S与x的函数关系式及x值的取值范围;(2)、要围成面积为45m2的花圃,AB的长是多少米?20. 如图,某大楼的顶部竖有一块广告牌CD,小马同学在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡比i=1: , AB=10米,AE=21米.(测角器的高度忽略不计,参考数据:sin53°
(1)、求S与x的函数关系式及x值的取值范围;(2)、要围成面积为45m2的花圃,AB的长是多少米?20. 如图,某大楼的顶部竖有一块广告牌CD,小马同学在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡比i=1: , AB=10米,AE=21米.(测角器的高度忽略不计,参考数据:sin53°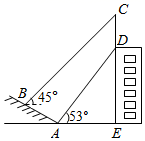 (1)、求点B距水平地面AE的高度;(2)、求广告牌的高度CD的长度.(结果保留根号)21. 如图,已知A(﹣5,n),B(3,﹣5)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)、求点B距水平地面AE的高度;(2)、求广告牌的高度CD的长度.(结果保留根号)21. 如图,已知A(﹣5,n),B(3,﹣5)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.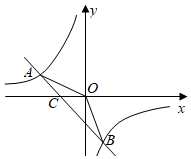 (1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、结合图象,直接写出不等式kx+b﹣<0的解集.22. 已知关于x的抛物线y=mx2﹣4mx+3m(m≠0)与x轴交于点B,C(点B位于点C左侧),与y轴交于点A.(1)、若该抛物线经过(﹣1,8),(1,4),(3,10)三点中的一点.
(1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、结合图象,直接写出不等式kx+b﹣<0的解集.22. 已知关于x的抛物线y=mx2﹣4mx+3m(m≠0)与x轴交于点B,C(点B位于点C左侧),与y轴交于点A.(1)、若该抛物线经过(﹣1,8),(1,4),(3,10)三点中的一点.①求m的值;
②直线AB的表达式;
(2)、当﹣13时,y有最小值﹣3,求此时抛物线的解析式.23. 如图1,在正方形ABCD中,射线AE,AF分别交BD于点G,H,交BC,CD于点E,F,且∠EAF=45°.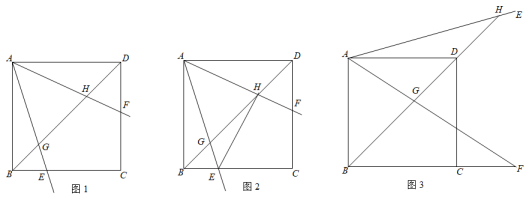 (1)、证明:AH•FH=DH•GH;(2)、如图2,连接EH,证明:△AEH是等腰直角三角形;(3)、如图3,∠EAF=45°,且它的两边分别与BC,BD的延长线交于点F,H,探索AH与AF之间的数量关系并加以说明.
(1)、证明:AH•FH=DH•GH;(2)、如图2,连接EH,证明:△AEH是等腰直角三角形;(3)、如图3,∠EAF=45°,且它的两边分别与BC,BD的延长线交于点F,H,探索AH与AF之间的数量关系并加以说明.