辽宁省沈阳市铁西区2021-2022学年八年级上学期12月月考数学试题

试卷更新日期：2022-01-04 类型：月考试卷

进入出卷网下载

一、单选题

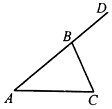
1. 下列实数中，无理数是（）

A、﹣2 B、0 C、 $\sqrt{5}$ D、3.14

查看试题解析
2. 一次函数y＝﹣x﹣2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，∠A＝40°，∠CBD是 $△$ ABC的外角，∠CBD＝110°，则∠C的大小（）

A、40° B、50° C、70° D、90°

查看试题解析
4. 若正比例函数y＝2x的图象经过点M(a﹣1，4)，则a的值为（）

A、0 B、1 C、2 D、3

查看试题解析
5. 已知方程组 ${\begin{array}{l} 2 x + 3 y = 16 \\ x + 4 y = 13 \end{array}$ ，则 $x - y =$ （）

A、5 B、2 C、3 D、4

查看试题解析
6. 甲、乙、丙、丁4名同学参加跳远测试各10次，他们的平均成绩及方差如表：
测试者
平均成绩（单位：m）
方差
甲
6.2
0.25
乙
6.0
0.58
丙
5.8
0.12
丁
6.2
0.32
若从其中选出1名成绩好且发挥稳定的同学参加学校运动会，则应选（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图，在平面直角坐标系中，一次函数y＝kx+b（k≠0）和y＝mx+n（m≠0）相交于点(2，﹣1)，则关于x，y的方程组 ${\begin{array}{l} k x = y - b \\ m x + n = y \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$

查看试题解析
8. 如图，若点 $A (1 ， 2)$ ，点 $B (- 2 ， - 1)$ ，在x轴上找一点P，使 $| P A - P B |$ 最小，则点P坐标为（）

A、（－5，0） B、（－1，0） C、（0，0） D、（1，0）

查看试题解析
9. 某校举行篮球赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场，负y场，则根据题意，下列方程组中正确的是（）

A、 ${\begin{array}{l} x + y = 26 \\ x + 2 y = 16 \end{array}$ B、 ${\begin{array}{l} x + y = 26 \\ 2 x + y = 16 \end{array}$ C、 ${\begin{array}{l} x + y = 16 \\ x + 2 y = 26 \end{array}$ D、 ${\begin{array}{l} x + y = 16 \\ 2 x + y = 26 \end{array}$

查看试题解析
10. 如图，四边形ABCD中，AB＝3cm，AD＝4cm，BC＝13cm，CD＝12cm，且∠A＝90°，则四边形ABCD的面积为（）

A、12cm² B、18cm² C、22cm² D、36cm²

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
12. 某中学规定学生的学期体育成绩满分为100，其中体育课外活动占30%，期末考试成绩占70%，小彤的这两项成绩依次是90，80.则小彤这学期的体育成绩是.

查看试题解析
13. 已知点 $A (- \frac{1}{2} ， m)$ ，点B(2，n)在直线y＝3x+b上，则m与n的大小关系是mn（填“＞”“＜”或“＝”）．

查看试题解析
14. 如图，直线l₁∥l₂ ，以直线l₁上的点A为圆心，适当长为半径在右侧画弧，分别交l₁ ， l₂于点B，C，连结AC，BC，若∠ABC＝70°，则∠1＝．

查看试题解析
15. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{4}{3}$ x+4与x轴、y轴分别交于A、B两点，点C在第二象限，若BC＝OC＝OA，则点C的坐标为．

查看试题解析
16. 如图，矩形ABCD中，AB＝9，AD＝12，点M在对角线BD上，点N为射线BC上一动点，连接MN，DN，且∠DNM＝∠DBC，当 $△$ DMN是等腰三角形时，线段BN的长为．

查看试题解析

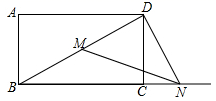
三、解答题

17. 计算： $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

查看试题解析
18. 解二元一次方程组： ${\begin{array}{l} x - 2 y = 5 \\ 3 x - 2 y = 8 \end{array}$ ．

查看试题解析
19. 如图， $△$ ABC三个顶点的坐标分别为A(﹣4，1)，B(﹣1，3)，C(﹣3，4)．

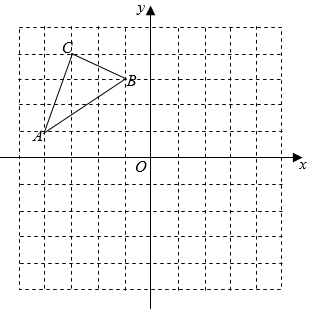(1)、请画出 $△$ ABC关于y轴对称的 $△$ A₁B₁C₁（点A，B，C的对应点分别是A₁ ， B₁ ， C₁），并直接写出点A₁的坐标；

(2)、 $△$ A₁B₁C₁中A₁C₁边上的高的长为个单位长度．

查看试题解析
20. 为迎接中国共产党建党100周年，某校开展了以“不忘初心跟党走”为主题的读书活动，学校对本校八年级学生9月份“阅读该主题相关书籍的读书量”（简称“读书量”）进行了随机抽样调查，对所有随机抽取学生的“读书量”（单位：本）进行了统计，并将调查结果绘制成如下两幅不完整的统计图．

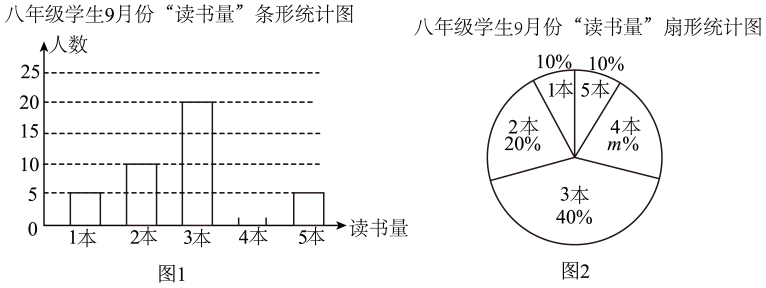(1)、请直接补全条形统计图；

(2)、本次所抽取学生9月份“读书量”的众数为本，中位数为本；

(3)、根据抽样调查的结果，请你估计该校八年级1000名学生中，9月份“读书量”不少于4本的学生人数．

查看试题解析
21. 两个直角三角板如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AB与DF交于点M，BC $∥$ EF，求∠BMD的度数．

查看试题解析
22. 某酒店有三人间客房和双人间客房，收费标准：一间三人间每天150元，一间双人间每天140元．为了吸引游客，酒店实行团体入住五折优惠措施，一个46人的旅游团优惠期间到该酒店入住，住了一些三人间和双人间客房，若每间客房正好住满，且一天共花去住宿费1 310元，则该旅游团住了三人间和双人间客房各多少间？

查看试题解析
23. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系如图所示．

(1)、A，B两城相距千米；

(2)、当1≤t≤4时，求乙车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系式；

(3)、乙车出发后小时追上甲车．

查看试题解析
24. 如图，已知四边形ABCD是正方形，点E是AD边上的一点（不与点A，D重合），连接CE，以CE为一边作正方形CEFG，使点F，G与点A，B在CE的两侧，连接BE并延长，交GD延长线于点H．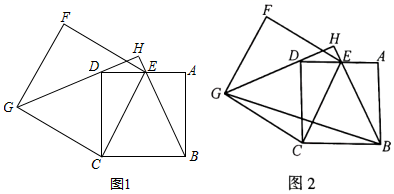
　

(1)、如图1，请判断线段BE与GD的数量关系和位置关系，并说明理由；

(2)、如图2，连接BG，若AB＝2，CE＝ $\sqrt{5}$ ，请你直接写出 $\sqrt{D E^{2} + B G^{2}}$ 的值．

查看试题解析
25. 如图，在平面直角坐标系中，点O是坐标原点，直线y＝﹣ $\frac{3}{4}$ x+6与x轴交于点A，与y轴交于点B，与直线y＝ $\frac{3}{4}$ x交于点C．

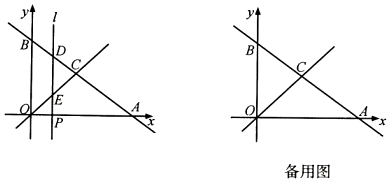(1)、求点C的坐标；

(2)、点P是线段OA上的一个动点（点P不与点O，A重合），过点P作平行于y轴的直线l，分别交直线AB，OC于点D，点E，设点P的横坐标为m．
①求线段PD的长（用含m的代数式表示）；
②当点P，D，E三点中有一个点是另两个点构成线段的中点时，请直接写出m的值；

(3)、过点C作CF⊥y轴于点F，点M在线段CF上且不与点C重合，点N在线段OC上，CM＝ON，连接BM，BN，BM+BN是否存在最小值？如果存在，请直接写出最小值；如果不存在，请说明理由．

查看试题解析

测试者	平均成绩（单位：m）	方差
甲	6.2	0.25
乙	6.0	0.58
丙	5.8	0.12
丁	6.2	0.32