2021-2022学年度第一学期八年级数学第11、12章 期末复习练习卷（人教版）
试卷更新日期：2022-01-03 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，∠A=70°，∠C=30°，BD平分∠ABC交AC于点D，DE∥AB，交BC于点E，则∠BDE的度数是（ ）
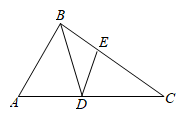A、30° B、40° C、50° D、60°2. 如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（ ）
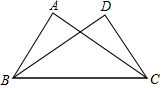A、∠ABC＝∠DCB B、∠ABD＝∠DCA C、AC＝DB D、AB＝DC3. 如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（ ）
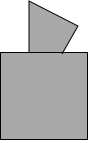A、SSS B、SAS C、AAS D、ASA4. 一块三角形玻璃被打碎后，店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃，能够全等的依据是（ ）
A、 B、 C、 D、5. 如图， 的角平分线 、 相交于 ， ， ，且 于 ，下列结论：① ；② ；③ 平分 ；④ .其中正确的结论的个数是（ ）.
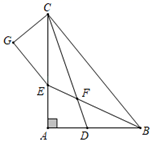A、1 B、2 C、3 D、46. 如图，△ABC中，∠C=75°，若沿图中虚线截去∠C，则∠1+∠2=（ ）
A、360° B、180° C、255° D、145°7. 如图O是 内的一点，且O到三边AB、BC、CA的距离 ．若 ，则 （ ）．
A、125° B、135° C、105° D、100°8. 如图，∠A=32°，∠B=45°，∠C=38°，则∠DFE等于（ ）
A、105° B、120° C、110° D、115°9. 如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（ ）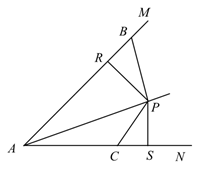
A、①② B、②③ C、①③ D、①②③10. 如图，点 ， 分别是 的边 ， 上的点， ， 相交于点 ，现给出下面两个结论，①当 ， 是 的中线时， ；②当 ， 是 的角平分线时， ，下列说法正确的是（ ）
A、只有①正确 B、只有②正确 C、①②都正确 D、①②都错误二、填空题
-
11. 如图，足球图片正中的黑色正五边形的外角和是°.
12. 任意五边形的内角和与外角和的差为度.13. 如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DC=3，则点D到AB的距离是
14. 如图，四边形 中， ，请补充一个条件 ， 使 ．
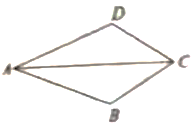15. 如图，在 ABC中，AH是高，AE BC，AB＝AE，在AB边上取点D，连接DE，DE＝AC，若 ，BH＝1，则BC＝.
三、解答题
-
16. 如图，已知∠ACB = ∠DCE，AC = BC，CD = CE，AD交BC于点F，连接BE，求证∠A = ∠B.
17. 如图， 中，∠A=30°，∠B=70°，CE平分∠ACB交AB于点E，CD是AB边上的高，求：∠DCE的度数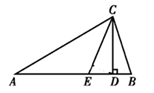
18. 如图，A、D、F、B在同一直线上，AD＝BF，AE＝BC，且AE//BC.求证：EF＝CD.
19. 已知：如图，AB∥ED，点F、点C在AD上，AB=DE，AF=DC.求证：BC=EF.
20. 已知：如图， ， 平分 ， 平分 ，交 于点 ， 于点 ，求证：点 到 与 的距离相等.
21. 已知点C和点F在线段BE上，且AB＝DE，∠B＝∠E，BC＝EF，AC和DF相交于点G．求证：AC＝DF．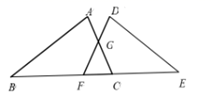
22. （问题背景）在四边形 中， ， ， ， 、 分别是 、 上的点，且 ，试探究图1中线段 、 、 之间的数量关系．
（初步探索）
小晨同学认为：延长 到点 ，使 ，连接 ，先证明 ，再证明 ，则可得到 、 、 之间的数量关系是 ．
（探索延伸）
在四边形 中如图2， ， ， 、 分别是 、 上的点， ，上述结论是否仍然成立？说明理由．
（结论运用）
如图3，在某次南海海域军事演习中，舰艇甲在指挥中心（ 处）北偏西30°的 处，舰艇乙在指挥中心南偏东70°的 处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以80海里/小时的速度前进，舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后，指挥中心观测到甲、乙两舰艇分别到达 ， 处，且两舰艇之间的夹角（ ）为70°，试求此时两舰艇之间的距离．