2021-2022学年浙教版数学八上各地期末优生突击训练

试卷更新日期：2022-01-03 类型：复习试卷

进入出卷网下载

一、综合题

1. 如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE．

(1)、请判断：AF与BE的数量关系是，位置关系是；

(2)、如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC，第（1）问中的结论是否仍然成立？请作出判断并给予说明；

(3)、若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．

查看试题解析
2. 如图，在平面直角坐标系中，点A(-4，0)，C(3，0)，D(0，4)， AG⊥CD于点G，交y轴于点B.

(1)、求证：△AOB≌△DOC．

(2)、点E在线段AB上，作OF⊥OE交CD于点F，连结EF．
①若E是AB的中点，求△OEF的面积.

②连结DE，当△DEF是以DE为腰的等腰三角形时，求CF的长．

查看试题解析
3. 如图，在△ABC中，AB=AC，CD⊥AB于点D，过点D作DE⊥BC于点E，交CA的延长线于点F．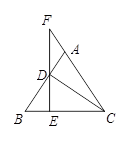

(1)、求证：△ADF是等腰三角形．

(2)、当CD $=$ 8，CF=10时，求BD的长．

查看试题解析
4. 如图， $A B = A E$ ， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ， $∠ B = 60 °$ ．

(1)、试说明： $△ A B C ≌ △ A E D$ ；

(2)、求 $∠ A E D$ 的度数．

查看试题解析
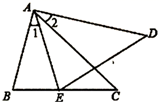5. 如图，在等腰 $△$ ABC中，AB=AC=6cm，∠B=30°，点D在BC边上由点C向点B匀速运动（点D不与点B ， C重合），速度为2cm/s，连接AD ，作∠ADE=30°，DE交线段AC于点E ．

(1)、在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA=75°，则∠BAD=°．

(2)、点D运动3s后到达图2位置，则CD=cm．此时 $△$ ABD和 $△$ DCE是否全等，请说明理由．

(3)、在点D运动过程中， $△$ ADE的形状也在变化．当 $△$ ADE是等腰三角形时，∠BDA的度数为．

查看试题解析
6.

(1)、如图1，在 $△$ ABC中，∠B=40°，∠C=60°，AD⊥BC于点D ， AE是∠BAC的平分线，求∠DAE的度数．

(2)、如图2，点E ， F在BC上，BE=CF ， AB=DC ， ∠B=∠C ．求证：∠A=∠D ．

查看试题解析
7. 有一种牛奶软包装盒如图1所示．为了生产这种包装盒，需要先画出展开图纸样．

(1)、如图2给出三种纸样甲、乙、丙，在甲、乙、丙中，正确的有．

(2)、利用你所选的一种纸样，求出包装盒的侧面积和表面积（侧面积与两个底面积的和）

查看试题解析
8. 一架长为 $10$ 米的梯子 $A B$ ，顶端 $B$ 靠在墙上，梯子底端 $A$ 到墙的距离 $A C = 6$ 米．

(1)、求 $B C$ 的长；

(2)、如图梯子的顶端 $B$ 沿墙向下滑动 $3$ 米，问梯子的底端 $A$ 向外移动了多少米？

查看试题解析
9. 定义：顶角相等且顶点重合的两个等腰三角形叫做对顶三角形．如图1，在 $△$ OAB与 $△$ OCD中，OA=OB ， OC=OD ， ∠AOB=∠COD ．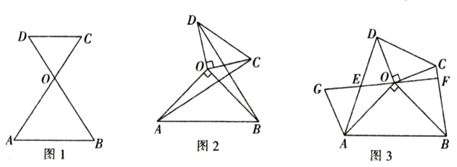

(1)、如图1， $△$ OAB与 $△$ OCD是对顶三角形，且A ， O ， C三点共线请判断AB与CD的位置关系，并说明理由．

(2)、如图2， $△$ OAB与 $△$ OCD是对顶三角形，∠AOB=∠COD=90°，连接AC ， BD ，试探究线段AC ， BD之间的关系，并说明理由．

(3)、如图3， $△$ OAB与 $△$ OCD是对顶三角形，∠AOB=∠COD=90°，连接AD ， BC ，取AD的中点E ，连接EO并延长交BC于点F ，延长OE至点G ，使EG=OE ，连接AG ，求证：EF⊥BC ．

查看试题解析
10. 已知点P在∠MON内．

(1)、如图1，点P关于射线OM的对称点是G，点P关于射线ON的对称点是H，连接OG、OH、OP．
①若∠MON=50°，则∠GOH= ▲ ；

②若PO=5，连接GH，请说明当∠MON为多少度时，GH=10；

(2)、如图2，若∠MON=60°，A、B分别是射线OM、ON上的任意一点，当 $△$ PAB的周长最小时，求∠APB的度数．

查看试题解析
11. 如图1，点A、D在y轴正半轴上，点B、C分别在x轴上，CD平分∠ACB与y轴交于D点，∠CAO＝90°﹣∠BDO ．

(1)、求证：AC＝BC；

(2)、如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA＝∠DBO ，求BC+EC的长．

查看试题解析
12. $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点 $D$ 是直线 $A B$ 上的一动点（不和 $A 、 B$ 重合）， $B E ⊥ C D$ 交 $C D$ 所在的直线于点 $E$ ，交直线 $A C$ 于 $F$ ．

(1)、点 $D$ 在边 $A B$ 上时，如图，试探索 $A B 、 F A$ 和 $B D$ 之间的等量关系，并说明理由；

(2)、点 $D$ 在 $A B$ 的延长线或反向延长线上时，请选择一种情况，画出图形，写出 $A B 、 F A$ 和 $B D$ 之间的等量关系，并说明理由．

查看试题解析
13. 如图1，在△ABC中，AE⊥BC于E ， AE＝BE ， D是AE上一点，且DE＝CE ，连接BD ， CD ．

(1)、判断 $B D$ 与 $A C$ 的位置关系和数量关系，并证明；

(2)、如图2，若将△DCE绕点E旋转一定的角度后，BD与AC的位置关系和数量关系是否发生变化？并证明；

(3)、如图3，将（2）中的等腰直角三角形都换成等边三角形，其他条件不变，求BD与AC夹角的度数．

查看试题解析
14. （背景介绍）勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．

（小试牛刀）把两个全等的直角三角形△ABC和△DAE如图1放置，其三边长分别为a ， b ， c ．显然，∠DAB＝∠B＝90°，AC⊥DE ．请用a ， b ， c分别表示出梯形ABCD ，四边形AECD ， △EBC的面积：

S_梯形ABCD＝，

S_△EBC＝，

S_{四边形AECD}＝，

再探究这三个图形面积之间的关系，它们满足的关系式为，化简后，可得到勾股定理．

（知识运用）

如图2，河道上A ， B两点（看作直线上的两点）相距200米，C ， D为两个菜园（看作两个点），AD⊥AB ， BC⊥AB ，垂足分别为A ， B ， AD＝80米，BC＝70米，现在菜农要在AB上确定一个抽水点P ，使得抽水点P到两个菜园C ， D的距离和最短，则该最短距离为米．

（知识迁移）

借助上面的思考过程，请直接写出当0＜x＜15时，代数式 $\sqrt{x^{2} + 9} + \sqrt{{(15 - x)}^{2} + 25}$ 的最小值＝．

查看试题解析
15. 在学习完第十二章后，刘老师让同学们独立完成识本56页第9题：如图1，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ，垂足分别为D ， E ． AD＝2.5cm，DE＝1.7cm，求BE的长．

(1)、请你也独立完成这道题；

(2)、待同学们完成这道题后，刘老师又出示了一道题：在课本原题其它条件不变的前提下，将CE所在直线旋转到△ABC的外部（如图2），请你猜想AD ， DE ， BE三者之间的数量关系，直接写出结论，不需证明．

(3)、如图3，将（1）中的条件改为：在△ABC中，AC＝BC ， D ， C ， E三点在同一条直线上，并且有∠BEC＝∠ADC＝∠BCA＝α，其中α为任意纯角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．

查看试题解析
16. 如图，C为线段BD上一动点，分别过点B、D作 $A B ⊥ B D$ ， $E D ⊥ B D$ ，连接AC、EC ．已知 $A B = 3$ ， $D E = 2$ ， $B D = 12$ ，设 $C D = x$ ．

(1)、用含x的代数式表示 $A C + C E$ 的长．

(2)、请问点C满足什么条件时， $A C + C E$ 的值最小，并求出此时 $A C + C E$ 的最小值．

(3)、根据（2）中的规律和结论，重新构图求出代数式 $\sqrt{x^{2} + 1} + \sqrt{{(8 - x)}^{2} + 25}$ 的最小值．

查看试题解析
17. （模型感知）

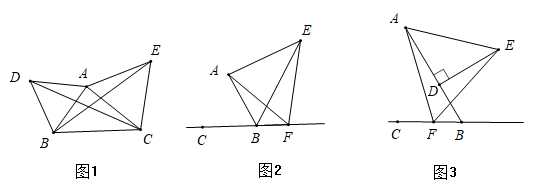(1)、如图1， $△ A B D$ 和 $△ A E C$ 都是等边三角形，求证， $B E = D C$ ；

(2)、（模型应用）
如图2，已知 $∠ A B C = 60 °$ ，点F在直线BC上，以AF为边作等边三角形AEF ，连接BE ，求证： $A B + B F = B E$ ；

(3)、（类比探究）
在（2）的条件下，当点F运动到射线BC上时，过点E作 $E D ⊥ A B$ 于点D ，请直接写出线段AB ， BF与BD之间存在的数量关系．

查看试题解析
18. 如图，点 $О$ 是等边 $△ A B C$ 内的一点， $∠ A O B = 110 ° ， ∠ B O C = α$ ．以 $O C$ 为边作等边 $△ O C D$ ，使 $△ O C D$ 和 $△ A B C$ 在直线 $B C$ 的同侧，连接 $A D$ ．

(1)、 $△ A D C$ 与 $△ B O C$ 全等吗?说明你的理由；

(2)、当 $α = 150 °$ 时，试判断 $△ A O D$ 的形状，并说明理由；

(3)、当 $α$ 为多少度时， $△ A O D$ 是等腰三角形?请直接写出答案．

查看试题解析
19. 已知：CD是经过∠BCA的顶点C的一条直线，CA＝CB ， E、F是直线CD上两点，∠BEC＝∠CFA＝∠α．

(1)、若直线CD经过∠BCA的内部，∠BCD＞∠ACD ．
①如图1，∠BCA＝90°，∠α＝90°，写出BE ， EF ， AF间的等量关系：．

②如图2，∠α与∠BCA具有怎样的数量关系，能使①中的结论仍然成立？写出∠α与∠BCA的数量关系．

(2)、如图3．若直线CD经过∠BCA的外部，∠α＝∠BCA ， ①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．

查看试题解析
20. 如图，在平面直角坐标系中，函数y＝－x＋2的图象与x轴，y轴分别交于点A ， B ，与函数y＝ $\frac{1}{3}$ x＋b的图象交于点C（－2，m）．

(1)、求m和b的值；

(2)、函数y＝－x＋b的图象与x轴交于点D ，点E从点D出发沿DA向，以每秒2个单位长度匀速运动到点M（到A停止运动），设点E的运动时间为t秒．
①当ΔACE的面积为12时，求t的值；

②在点E运动过程中，是否存在t的值，使ΔACE为直角三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析
21. 某天中午，小明从文具店步行返回学校，与此同时，小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计)，然后原路返回学校，两人均匀速行驶，结果两人同时到达学校．小明、小亮两人离书店的路程y₁、y₂(单位：米)与出发时间x(单位：分)之间的函数图象如图所示．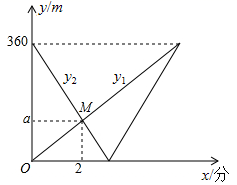

(1)、学校和文具店之间的路程是米，小亮的速度是小明速度的倍；

(2)、求a的值，并解释图中点M的横坐标、纵坐标的实际意义；

(3)、小明与小亮迎面相遇以后，再经过多长时间两人相距20米？

查看试题解析
22.

(1)、如图①在 $△$ ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②∠CBO= $\frac{1}{3}$ ∠ABC，∠BCO= $\frac{1}{3}$ ∠ACB，∠A=α，则∠BOC=（用α表示）

(2)、扩展探究：
如图③，∠CBO= $\frac{1}{3}$ ∠DBC，∠BCO= $\frac{1}{3}$ ∠ECB，∠A=α，求∠BOC的度数（用α表示），并说明理由.

查看试题解析
23. 在△ABC中，∠C＝90°，点D在边AC上，过点A作AE⊥AB交BD的延长线于E，过点E作EM⊥AC于M，且AE＝AD，∠AED＝∠ADE.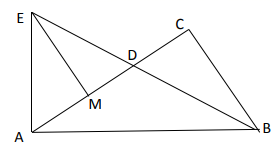

(1)、如果∠CAB＝36°，求∠CBD的度数；

(2)、求证：AB＝EM＋BC

查看试题解析
24. 如图，在等边△ABC中，点E为边AB上任意一点，点D在边CB的延长线上，且ED＝EC.

(1)、当点E为AB的中点时（如图1），则有AEDB（填“＞”“＜”或“＝”）；

(2)、猜想AE与DB的数量关系，并证明你的猜想.

查看试题解析
25. 在△ABC中，∠ABC＝∠ACB ，点D在直线BC上（不与B、C重合），点E在直线AC上（不与A、C重合），且∠ADE＝∠AED ．

(1)、如图1，若∠ABC＝50°，∠AED＝80°，则∠CDE＝°，此时， $\frac{∠ B A D}{∠ C D E}$ ＝．

(2)、若点D在BC边上（点B、C除外）运动（如图1），试探究∠BAD与∠CDE的数量关系，并说明理由；

(3)、若点D在线段BC的延长线上，点E在线段AC的延长线上（如图2），其余条件不变，请直接写出∠BAD与∠CDE的数量关系：．

(4)、若点D在线段CB的延长线上（如图3），点E在直线AC上，∠BAD＝26°，其余条件不变，则∠CDE＝（友情提醒：可利用图3画图分析）．

查看试题解析
26. 如图，在平面直角坐标系中，一次函数 $y = k_{1} x + b$ 的图象与 $x$ 轴交于点 $A (- 3 ， 0)$ ，与 $y$ 轴交于点B，且与正比例函数 $y = k_{2} x$ 的图象交点为 $C (3 ， 4)$ .

(1)、求正比例函数与一次函数的关系式.

(2)、若点D在第二象限， $△ D A B$ 是以AB为直角边的等腰直角三角形，请求出点D的坐标.

(3)、在 $y$ 轴上是否存在一点P使 $△ P O C$ 为等腰三角形，若存在，求出所有符合条件的点P的坐标.

查看试题解析