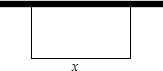2021-2022学年度第一学期九年级数学 期末总复习练习卷二(人教版)
试卷更新日期:2022-01-03 类型:复习试卷
一、单选题
-
1. 如图,AB、CD是⊙O的两条弦,连结AD、BC . 若∠BCD=70°,则∠BAD的度数为( )
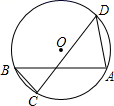 A、40° B、50° C、60° D、70°2. 方程 的根是( )A、 B、 C、 , D、 ,3. ⊙O的直径为9,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定4. 如图,已知 是半圆 的直径, , 是 的中点,那么 的度数是( )
A、40° B、50° C、60° D、70°2. 方程 的根是( )A、 B、 C、 , D、 ,3. ⊙O的直径为9,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定4. 如图,已知 是半圆 的直径, , 是 的中点,那么 的度数是( )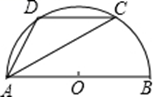 A、 B、 C、 D、5. 一元二次方程x2﹣4x+3=0的根是( )A、﹣1 B、﹣3 C、1和3 D、﹣1和﹣36. 若点P关于x轴对称的点为 ,则点P关于原点对称的点的坐标为( )A、 B、 C、 D、7. 如图,点A、B、C都在⊙O上,若∠AOB=76°,则∠ACB的度数为( )
A、 B、 C、 D、5. 一元二次方程x2﹣4x+3=0的根是( )A、﹣1 B、﹣3 C、1和3 D、﹣1和﹣36. 若点P关于x轴对称的点为 ,则点P关于原点对称的点的坐标为( )A、 B、 C、 D、7. 如图,点A、B、C都在⊙O上,若∠AOB=76°,则∠ACB的度数为( )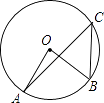 A、19° B、30° C、38° D、76°8. 点P(x,y)在第二象限内,且|x|=2,|y|=3,则点P关于原点对称的点的坐标为( )A、(2,-3) B、(-2,-3) C、(3,-2) D、(-3,2)9.
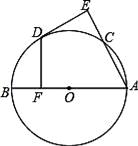
A、19° B、30° C、38° D、76°8. 点P(x,y)在第二象限内,且|x|=2,|y|=3,则点P关于原点对称的点的坐标为( )A、(2,-3) B、(-2,-3) C、(3,-2) D、(-3,2)9.如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、 为半径的圆的位置关系是( )
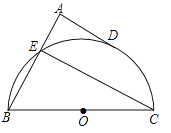 A、相切 B、相交 C、相离 D、无法确定10.
A、相切 B、相交 C、相离 D、无法确定10.如图,正方形ABCD的边长为1,E、F分别是边BC和CD上的动点(不与正方形的顶点重合),不管E、F怎样动,始终保持AE⊥EF . 设BE=x , DF=y , 则y是x的函数,函数关系式是( )
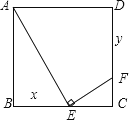 A、y=x+1 B、y=x-1 C、y=x2-x+1 D、y=x2-x-1
A、y=x+1 B、y=x-1 C、y=x2-x+1 D、y=x2-x-1二、填空题
-
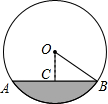
11. 从n个苹果和4个雪梨中,任选1个,若选中苹果的概率是 ,则n的值是.12. 方程x2﹣4x=0的解为.13. 在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .14. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是 .
 15. 如图,等腰直角三角形 中,点A、点B分别在y轴、x轴上,且 . 将 绕点B顺时针旋转使斜边 落在x轴上,得到第一个 ;将 绕点 顺时针旋转使边 落在x轴上,得到第二个 ;将 绕点 顺时针旋转使边 落在x轴上,得到第三个 ;……顺次这样做下去,得到的第2019个三角形落在x轴上的边的右侧顶点所走的路程为 .
15. 如图,等腰直角三角形 中,点A、点B分别在y轴、x轴上,且 . 将 绕点B顺时针旋转使斜边 落在x轴上,得到第一个 ;将 绕点 顺时针旋转使边 落在x轴上,得到第二个 ;将 绕点 顺时针旋转使边 落在x轴上,得到第三个 ;……顺次这样做下去,得到的第2019个三角形落在x轴上的边的右侧顶点所走的路程为 .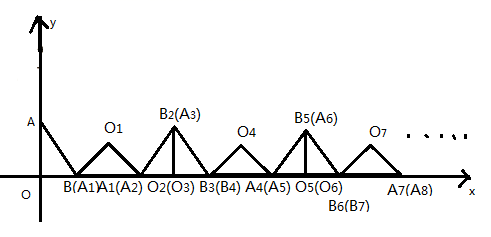
三、解答题
-
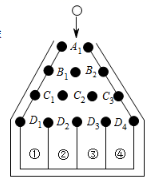
16. 如图,是一个竖直放置的钉板,其中,黑色圆面表示钉板上的钉子, 分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入口 处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入下面的某个槽内.用画树状图的方法,求圆球落入③号槽内的概率.
 17. 如图,弦CD垂直于⊙O的直径AB,垂足为P,且CD=2 ,BP=1,求⊙O的半径.
17. 如图,弦CD垂直于⊙O的直径AB,垂足为P,且CD=2 ,BP=1,求⊙O的半径. 18. 已知 是关于x的一元二次方程 的两个不相等的实数根,且满足 ,求m的值.19. 体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号)
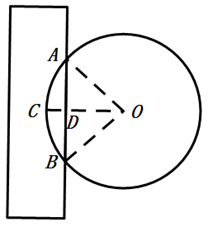
18. 已知 是关于x的一元二次方程 的两个不相等的实数根,且满足 ,求m的值.19. 体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号)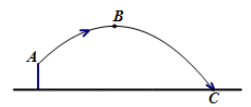 20. 《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锡口深1寸,锯道长1尺.如图,已知弦 尺,弓形离 寸,(注:1尺 寸)问这块圆柱形木材的直径是多少寸?
20. 《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锡口深1寸,锯道长1尺.如图,已知弦 尺,弓形离 寸,(注:1尺 寸)问这块圆柱形木材的直径是多少寸?