2021-2022学年度第一学期九年级数学期末总复习练习卷一（人教版）

试卷更新日期：2022-01-03 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “射击运动员射击一次，命中靶心”这个事件是（）

A、确定事件 B、必然事件 C、不可能事件 D、随机事件

查看试题解析
3. 方程x（x+1）＝0的解是（）

A、x＝0 B、x＝1 C、x₁＝0，x₂＝1 D、x₁＝0，x₂＝﹣1

查看试题解析
4. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 有三把外观一样但型号不同的锁，各配有一把钥匙．现遗失一把钥匙，用剩余的两把钥匙各随机从三把锁中选一把开锁一次，两次都不能打开的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{4}{9}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图， $A B$ 是 $⊙ O$ 的直径，且 $A B = 4$ ， $C$ 是 $⊙ O$ 上一点，将 $\overset{⌢}{A C}$ 沿直线 $A C$ 翻折，若翻折后的圆弧恰好经过点 $O$ ，则图中阴影部分的面积为（）.

A、 $\frac{4 π}{3} - \sqrt{3}$ B、 $\frac{4 π}{3}$ C、 $\frac{8π}{3}$ D、 $\frac{2π}{3}$

查看试题解析
7. 将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个.若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1个，为了获得最大利润（）

A、5元 B、10元 C、15元 D、20元

查看试题解析
8. 下列关于 $x$ 的一元二次方程中，有两个不相等的实数根的方程是（）

A、 $x^{2} + 2 = 0$ B、 $2 x^{2} + 3 x + 2 = 0$ C、 $4 x^{2} - 12 x + 9 = 0$ D、 $3 x^{2} + 5 x - 8 = 0$

查看试题解析
9. 已知，抛物线y＝ax²＋2ax在其对称轴的左侧y随x的增大而减小，关于x的方程ax²＋2ax＝m（m＞0）的一个根为﹣4，而关于x的方程ax²＋2ax＝n（0＜n＜m）有两个整数根，则这两个根的积是（）

A、0 B、﹣3 C、﹣6 D、﹣8

查看试题解析
10. 在平面直角坐标系中，已知点 $A (- 2 ， 2)$ ， $B (2 ， 1)$ ，若抛物线 $y = a x^{2} - 2 x + 1 (a \neq 0)$ 与线段 $A B$ 有两个不同的交点，则 $a$ 的取值范围是（）

A、 $- \frac{49}{32} < a \leq - \frac{3}{4}$ 或 $a \geq 1$ B、 $a \geq - \frac{3}{4}$ 或 $a < - \frac{49}{32}$ C、 $- \frac{3}{4} \leq a \leq 1$ 且 $a \neq 0$ D、 $a \leq - \frac{3}{4}$ 或 $a \geq 1$

查看试题解析

二、填空题

11. 已知四边形 $A B C D$ 的四个顶点都在 $⊙ O$ 上，则得到结论 $∠ A + ∠ C = 180 °$ .上述推理由因到果的依据是.

查看试题解析
12. 方程 $x^{2} - 9 = 0$ 的根为．

查看试题解析
13. ⊙O内一点P到⊙O上的最近点的距离为2，最远点的距离为4，则⊙O的半径为 .

查看试题解析
14. 菱形 $A B C D$ 的两条对角线长为方程 $y^{2} - 12 y + 32 = 0$ 的一个根，则菱形 $A B C D$ 的周长为．

查看试题解析
15. 若关于x的方程(a+1)x²+(2a﹣3)x+a﹣2＝0有两个不相等的实根，且关于x的方程 $\frac{a x}{1 + x} - 1 = \frac{3}{x + 1}$ 的解为整数，则满足条件的所有整数a的和是．

查看试题解析

三、解答题

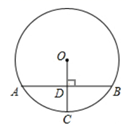
16. 如图，AB为⊙O的弦，AB=8，OC⊥AB于点D，交⊙O于点C，且CD=l ，求⊙O的半径.

查看试题解析
17. 判断关于 $x$ 的方程 $(x - 3) (x - 2) = p^{2}$ 根的情况，并说明理由.

查看试题解析
18. 解关于x的一元二次方程 $x^{2} - 8 = x (m x - 2)$ ，其中m是满足不等式组 ${\begin{array}{l} 4 m + 3 > 0 \\ 5 - 3 m > 0 \end{array}$ 的整数．

查看试题解析
19. 随着信息技术的发展，人们在购物时的支付方式多样且便捷可以用微信、支付宝、银行卡、现金四种方式在某商场购物的张老师可以随机的采用这四种方式中的任意一种结账.一天，他在这个商场有两次结账行为.请你用画树状图或列表格的方式，求出张老师两次结账采用不同方式的概率.

查看试题解析
20. 已知AB为 $⊙ O$ 的直径，EF切 $⊙ O$ 于点D ，过点B作 $B H ⊥ E F$ 于点H交 $⊙ O$ 于点C ，连接BD ．

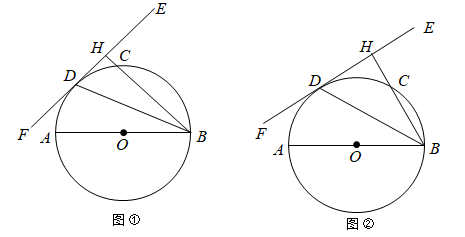(1)、如图①，若 $∠ B D H = 65 °$ ，求 $∠ A B H$ 的大小；

(2)、如图②，若C为弧BD的中点，求 $∠ A B H$ 的大小．

查看试题解析
21. 为促进经济发展，方便居民出行，某施工队要修建一个横断面为抛物线的公路隧道，隧道最高点P离路面 $O M$ 的距离为6米，宽度 $O M$ 为12米，隧道内设双向行车道，并且中间有一条宽为1米的隔离带.如果一货运汽车装载某大型设备后高为4米，宽为3.5米，按如图所示的平面直角坐标系这辆货车能否安全通过？为什么？

查看试题解析
22. 如图

（1）请画出△ABC关于原点O对称的△A₁B₁C₁；
（2）请画出△ABC绕点B逆时针旋转90°后的△A₂BC₂；
（3）写出A₂和C₂两点坐标．

查看试题解析

2021-2022学年度第一学期九年级数学 期末总复习练习卷一（人教版）

一、单选题

二、填空题

三、解答题

2021-2022学年度第一学期九年级数学期末总复习练习卷一（人教版）