2021-2022学年度第一学期九年级数学第25章《概略初步》25.1随机事件与概略 期末复习练习卷（人教版）
试卷更新日期：2022-01-03 类型：复习试卷
一、单选题
-
1. 任意一个事件发生的概率p的取值范围是（ ）A、0＜P＜1 B、0≤P＜1 C、0＜P≤1 D、0≤p≤12. 袋中装有10个黑球、5个红球，1个白球，它们除颜色外无差别，随机从袋子中摸出一球，则下列事件可能性最大的是（ ）A、摸到黄球 B、摸到白球 C、摸到红球 D、摸到黑球3. 下列事件中，随机事件的是（ ）A、掷骰子两次，点数和为13 B、在图形的旋转变换中，面积不会改变 C、经过城市某一个有交通信号灯的路口，遇到红灯 D、二月份有30天4. 下列说法错误的是（ ）A、打开电视剧，电视里播放《小猪佩奇》是偶然事件 B、了解一批灯泡的使用寿命，适合抽样调查 C、一元二次方程 只有一个根 D、甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是 ， ，甲的射击成绩稳定5. 下列事件中，是必然事件的是（ ）A、买一张电影票，座位号是3的倍数 B、一个盒子装有 个红球和 个白球，除颜色外其它完全相同，同时摸出两个球，一定会摸到红球 C、掷一枚质地均匀的硬币，正面向上 D、走过一个红绿灯路口时，前方正好是红灯6. 掷两枚质地均匀的硬币，两枚硬币全部正面朝上的概率是 （ ）A、 B、 C、 D、7. 如图，飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是（ ）
A、 B、 C、 D、8. 斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数列1，1，2，3，5，画出来的螺旋曲线．如图，白色小圆内切于边长为1的正方形，黑色曲线就是斐波那契螺旋线，它是依次在以1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将其圆弧连接起来得到的．若在矩形ABCD内随机取一点，则此点取自阴影部分的概率是（ ）
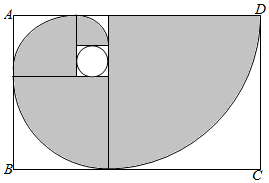A、 B、 C、 D、9. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干，这些糖果除颜色外无其他差别.具体情况如下表所示.袋子 糖果
红色
黄色
绿色
总计
甲袋
2颗
2颗
1颗
5颗
乙袋
4颗
2颗
4颗
10颗
若小明从甲、乙两个袋子中各随机摸出一颗糖果，则他从甲袋比从乙袋（ ）
A、摸出红色糖果的概率大 B、摸出红色糖果的概率小 C、摸出黄色糖果的概率大 D、摸出黄色糖果的概率小10. 从一盒写有“水果月饼2枚，巧克力月饼2枚，海苔月饼2枚，蛋黄月饼2枚”的礼饼盒里随机取出一枚，正好是巧克力月饼的概率是（ ）A、 B、 C、 D、二、填空题
-
11. 从标有1到20号的卡片中任意抽取一张，记事件“抽到2的倍数”发生的可能性为P (A)，事件“抽到5的倍数”发生的可能性为P(B) ，事件“ 抽到13的倍数" 发生的可能性为P(C)，请用“＞”连接P(A)，P(B)，P(C)为.12. 在一个不透明的袋子中装有2个红球、5个白球和3个黑球，这些球除颜色外都相同.从中任意摸出1个球，摸到色的球的可能性最大.(填“红”、“白”或“黑”)13. 下列事件：①任意画一个三角形，其内角和为180°；②在平面内任意画两条直线，则其位置关系是相交；③掷一枚质地均匀的骰子，向上一面的点数是6.其中是随机事件的是.（填序号）14. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是 ．
15. 把一转盘先分成两个半圆，再把其中一个半圆等分成三等份，并标上数字如图所示，任意转动转盘，当转盘停止时，指针落在偶数区域的概率是.
三、解答题
-
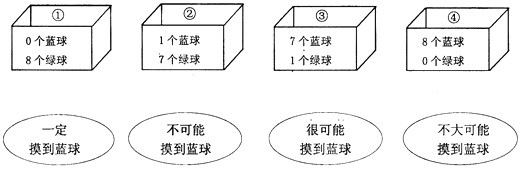
16. 下列第一排表示各盒中球的情况，第二排的语言描述了摸到篮球的可能性大小，请你用线把第一排盒子与第二排的描述连接起来使之相符．
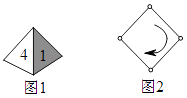
17. 下面第一排表示了十张扑克牌中不同情况，任意摸一张，请你用第二排的语言来描述摸到红色扑克牌的可能性大小，并用线连起来．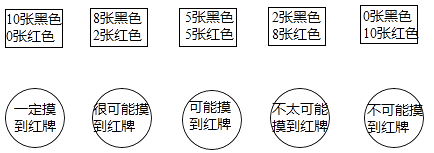
18. 如图1，一枚质地均匀的正四面体骰子，它有四个面．并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏则每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D．若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B．…设游戏这从圈A起跳．嘉嘉随机掷一次骰子．淇淇随机掷两次骰子．请问嘉嘉与淇淇掷完骰子落回到圈A的可能性一样吗？回答问题并说明理由．
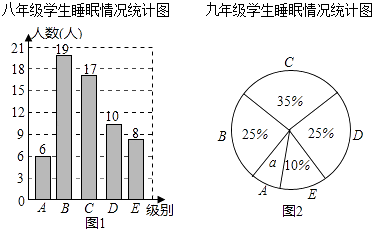
19.为了解某校八、九年级部分学生的睡眠情况，随机抽取了该校八、九年级部分学生进行调查，已知抽取的八年级与九年级的学生人数相同，利用抽样所得的数据绘制如图的统计图表：
睡眠情况分段情况如下
组别
睡眠时间x（小时）
A
4.5≤x＜5.5
B
5.5≤x＜6.5
C
6.5≤x＜7.5
D
7.5≤x＜8.5
E
8.5≤x＜9.5
根据图表提供的信息，回答下列问题：
（Ⅰ）直接写出统计图中a的值
（Ⅱ）睡眠时间少于6.5小时为严重睡眠不足，则从该校八、九年级各随机抽一名学生，被抽到的这两位学生睡眠严重不足的可能性分别有多大？
20. 如图所示，口袋中有5张完全相同的卡片，分别写有2cm，4cm，6cm，8cm和10cm，袋外有两张卡片，分别写有6cm和10cm，现随机从袋内取出一张卡片，与口袋外两张卡片放在一起，以卡片上的数量分别作为三条线段的长度，求这三条线段能构成等腰三角形的概率．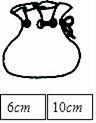
21. 如图，一个可以自由转动的转盘，分成了四个扇形区域，共有三种不同的颜色，其中红色区域扇形的圆心角为 .小华对小明说：“我们用这个转盘来做一个游戏，指针指向蓝色区域你赢，指针指向红色区域我赢”.你认为这个游戏规则公平吗？请说明理由.
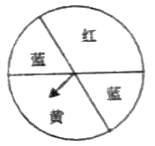22. 小明学习电学知识后，用四个开关按键（每个开关按键闭合的可能性相等）、一个电源和一个灯泡设计了一个电路图(1)、若小明设计的电路图如图1（四个开关按键都处于打开状态）如图所示，求任意闭合一个开关按键，灯泡能发光的概率；
(2)、若小明设计的电路图如图2（四个开关按键都处于打开状态）如图所示，求同时闭合其中的两个开关按键，灯泡能发光的概率．（用列表或树状图法）