湖南省部分校2021-2022学年高一上学期数学12月联考试卷
试卷更新日期:2021-12-31 类型:月考试卷
一、单选题
-
1. 设集合 , , , 则( )A、 B、 C、 D、2. 2021年1月初,中国多地出现散发病例甚至局部聚集性疫情,在此背景下,各地陆续发出“春节期间非必要不返乡”的倡议,鼓励企事业单位职工就地过年.某市针对非本市户籍并在本市缴纳社保,且春节期间在本市过年的外来务工人员,每人发放1000元疫情专项补贴.小张是该市的一名务工人员,则“他在该市过年”是“他可领取1000元疫情专项补贴”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 命题“ , ”的否定为( )A、 , B、 , C、 , D、 ,4. 函数的零点所在的区间为( )A、 B、 C、 D、5. 函数的部分图象大致为( )A、
 B、
B、 C、
C、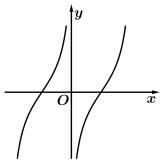 D、
D、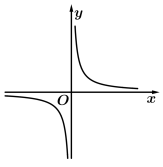 6. 已知 , 则( )A、 B、 C、 D、7. 心理学家有时用函数来测定人们在时间内能够记忆的单词量 , 其中表示需要记忆的单词量,表示记忆率.假设某学生有200个单词要记忆,心理学家测定在内该学生能够记忆20个单词,则该学生在内能记忆的单词个数约为( )A、69 B、65 C、67 D、638. 已知偶函数满足 , 且当时,若函数恰有4个零点,则( )A、2 B、3 C、4 D、5
6. 已知 , 则( )A、 B、 C、 D、7. 心理学家有时用函数来测定人们在时间内能够记忆的单词量 , 其中表示需要记忆的单词量,表示记忆率.假设某学生有200个单词要记忆,心理学家测定在内该学生能够记忆20个单词,则该学生在内能记忆的单词个数约为( )A、69 B、65 C、67 D、638. 已知偶函数满足 , 且当时,若函数恰有4个零点,则( )A、2 B、3 C、4 D、5二、多选题
-
9. 已知角的终边与单位圆交于点 , 则( )A、 B、 C、 D、10. 下列函数中,最小值为2的是( )A、 B、 C、 D、11. 已知函数 , 则( )A、的定义域为 B、的值域为 C、为减函数 D、为奇函数12. 已知函数 , 则 ( )A、若的最小值为-1,则 B、当时,恒成立 C、当时,存在且 , 使得 D、存在 , 使得对任意恒成立
三、填空题
-
13. 已知幂函数是偶函数,则 .14. 已知函数满足①定义域为;②值域为;③.写出一个满足上述条件的函数:.15. 已知为锐角,若 , 则 .16. 若对任意 , 总存在 , 使得 , 则的取值范围是.
四、解答题
-
17.(1)、计算的值;(2)、已知 , 计算的值.18. 已知 .(1)、求的值;(2)、求的值.19. 某公司今年年初用64万元收购了1个项目,若该公司从第1年到第(且)年花在该项目的其他费用(不包括收购费用)为万元,该项目每年运行的总收入为40万元.(1)、试问该项目运行到第几年开始盈利?(2)、该项目运行若干年后,公司提出了两种方案:
①当盈利总额最大时,以24万元的价格卖出;
②当年平均盈利最大时,以28万元的价格卖出.
假如要在这两种方案中选择一种,你会选择哪一种?请说明理由.