河北省邯郸市永年区2021-2022学年九年级上学期第一次三校联考数学试题

试卷更新日期：2021-12-29 类型：月考试卷

进入出卷网下载

一、单选题

1. 在一次数学答题比赛中，五位同学答对题目的个数分别为7，5，3，5，10，则关于这组数据的说法错误的是（　　）

A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.6

查看试题解析
2. 下列说法：（1）长度相等的弧是等弧；（2）弦不包括直径；（3）劣弧一定比优弧短；（4）直径是圆中最长的弦．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 点 $(- s i n 60 ° ， c o s 30 °)$ 关于y轴对称的点的坐标是（）

A、 $(- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ B、 $(\frac{1}{2} ， \frac{\sqrt{3}}{2})$ C、 $(\frac{\sqrt{3}}{2} ， \frac{\sqrt{3}}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， \frac{\sqrt{3}}{2})$

查看试题解析
4. 关于x的一元二次方程 $3 x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
5. 反比例函数 $y = - \frac{1}{x}$ ，下列说法错误的是（　　）

A、图象经过点（1，﹣1） B、图象位于第二、四象限 C、图象关于直线y＝﹣x对称 D、y随x的增大而增大

查看试题解析
6. 已知平面内有⊙O和点A ， B ，若⊙O半径为2cm ，线段OA＝3cm ， OB＝2cm ，则直线AB与⊙O的位置关系为（）

A、相离 B、相交 C、相切 D、相交或相切

查看试题解析
7. 如图，正六边形 $A B C D E F$ 的边长为6，以顶点A为圆心， $A B$ 的长为半径画圆，则图中阴影部分的面积为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $12 π$

查看试题解析
8. 若 $a b < 0$ ，则正比例函数y=ax与反比例函数 $y = \frac{b}{x}$ 在同一平面直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图，已知AB是⊙O的直径，CD是弦，若∠BCD=24°，则∠ABD=（）

A、54° B、56° C、64° D、66°

查看试题解析
10. 如图，在△ABC 中，∠C=90°，BC=6，D，E 分别在 AB、AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为（　　）

A、 $\frac{1}{2}$ B、2 C、3 D、4

查看试题解析
11. 若M（-2，a），N（2，b），P（4，c）三点都在函数y= $\frac{m^{2} + 1}{x}$ 的图象上，则a、b、c的大小关系为（）

A、a＞b＞c B、b＞c＞a C、c＞a＞b D、c＞b＞a

查看试题解析
12. 如图，在等腰△ABC中，∠BAC＝120°，AD是∠BAC的角平分线，且AD＝6，以点A为圆心，AD长为半径画弧 $\overset{⌢}{E F}$ ，交AB于点E，交AC于点F，将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高为（　　）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{2}$

查看试题解析
13.
如图，在平行四边形ABCD中，E是BC延长线上一点，AE交CD于点F，且CE= $\frac{1}{2}$ BC，则 $\frac{S_{△ A D F}}{S_{△ E B A}}$ =（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{4}{9}$

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ，点D在 $A C$ 上， $∠ D B C = ∠ A$ ．若 $A C = 4 ， c o s A = \frac{4}{5}$ ，则 $B D$ 的长度为（）

A、 $\frac{9}{4}$ B、 $\frac{12}{5}$ C、 $\frac{15}{4}$ D、 $4$

查看试题解析
15. 如图，在平面直角坐标系中， $R t Δ A B C$ 的顶点A，B分别在y轴、x轴上， $O A = 2$ ， $O B = 1$ ，斜边 $A C / / x$ 轴．若反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过 $A C$ 的中点D，则k的值为（）

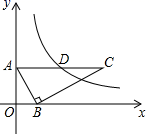A、4 B、5 C、6 D、8

查看试题解析
16. 如图，在等边△ABC中，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E，F是AC上的点，判断下列说法错误的是（　　）

A、若EF⊥AC，则EF是⊙O的切线 B、若EF是⊙O的切线，则EF⊥AC C、若BE＝EC，则AC是⊙O的切线 D、若 $B E = \frac{\sqrt{3}}{2} E C$ ，则AC是⊙O的切线

查看试题解析

二、填空题

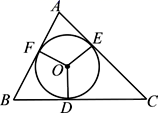
17. 将一元二次方程 $x^{2} - 6 x - 5 = 0$ 化成 $(x - a)^{2} = b$ 的形式，那么 $a + b$ 的值为．

查看试题解析
18. 如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=9cm，BC=14cm，CA=13cm，则AF的长为．

查看试题解析
19. 如图，正方形ABCD，边长为4，点P和点Q在正方形的边上运动，且PQ＝4，若点P从点B出发沿B→C→D→A的路线向点A运动，到点A停止运动；点Q从点A出发，沿A→B→C→D的路线向点D运动，到达点D停止运动．它们同时出发，且运动速度相同，则在运动过程中PQ的中点O所经过的路径长为．

查看试题解析

三、解答题

20. 某校要从甲、乙两名同学中挑选一人参加创新能力大赛，在最近的五次选拔测试中，他俩的成绩分别如下表，请根据表中数据解答下列问题：

	第 1 次	第 2 次	第 3 次	第 4 次	第 5 次	平均分	众数	中位数	方差
甲	60 分	75 分	100 分	90 分	75 分	80 分	75 分	75 分	190
乙	70 分	90 分	100 分	80 分	80 分		80 分	80 分

(1)、把表格补充完整：

(2)、在这五次测试中，成绩比较稳定的同学是多少；若将 80 分以上（含 80 分）的成绩视为优秀，则甲、乙两名同学在这五次测试中的优秀率分别是多少；

(3)、历届比赛表明，成绩达到80分以上（含 80分）就很可能获奖，成绩达到 90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．

查看试题解析

21. 如图，⊙O的直径AB垂直弦CD于点E，AB＝8，∠A＝22.5°，求CD的长．

查看试题解析
22. 如图，在四边形ABCD中，AC、BD相交于点F，点E在BD上，且 $\frac{A B}{A E} = \frac{B C}{E D} = \frac{A C}{A D}$ ．

(1)、∠1与∠2相等吗？为什么？

(2)、判断△ABE与△ACD是否相似？并说明理由．

查看试题解析
23. 某餐馆推出特色小吃，推出了“堂食”和“外卖”两种销售方式．当特色小吃以“外卖”方式售出时，餐馆需额外支付网络平台服务费，服务费为“外卖”销售额的20%．（注：收入＝销售额﹣服务费）根据以上信息，解决下列问题：

(1)、10月份，该餐馆需额外支付的服务费为元，该月收入为元；

(2)、经调研，该餐馆在10月份“堂食”600份销量的基础上，“堂食”价格每提高1元，“堂食”的销量就减少5份，但提高后的价格不能超过30元/份；“外卖”价格始终保持不变．该餐馆计划11月份只做800份特色小吃，预计全部售完．问“堂食”如何定价，11月份的收入是10760元？

查看试题解析
24. 为了预防“流感”，某学校对教室采用药熏法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与药物点燃后的时间x（分）成正比例，药物燃尽后，y与x成反比例（如图所示），已知药物点燃后6分钟燃尽，此时室内每立方米空气中含药量为12毫克．

(1)、求药物燃烧时和药物燃尽后，y与x之间的函数表达式；

(2)、研究表明：空气中每立方米的含药量不低于6毫克，且持续5分钟以上才能有效杀灭空气中的病菌，请计算说明此次消毒能否有效杀灭空气中的病菌．

查看试题解析
25. 汽车盲区是指驾驶员位于驾驶座位置，其视线被车体遮挡而不能直接观察到的区域．如图， $△ A B C$ 、 $△ F E D$ 分别为汽车两侧盲区的示意图，已知视线 $P B$ 与地面 $B E$ 的夹角 $∠ P B E = 45 °$ ，视线 $P E$ 与地面 $B E$ 的夹角 $∠ P E B = 20 °$ ，点A，F分别为 $P B$ ， $P E$ 与车窗底部的交点， $A F ∥ B E$ ， $A C$ ， $F D$ 垂直地面 $B E$ ， A点到B点的距离 $\sqrt{2} m$ ．（参考数据： $s i n 20 ° \approx 0.3$ ， $c o s 20 ° \approx 0.9$ ， $t a n 20 ° \approx 0.4$ ）

(1)、求盲区中 $D E$ 的长度；

(2)、点M在 $E D$ 上， $M D = 1.8 m$ ，在M处有一个高度为 $0.3 m$ 的物体，驾驶员能观察到物体吗？请说明．

查看试题解析
26. 如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．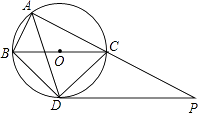

(1)、求证：PD是⊙O的切线；

(2)、求证：△ABD∽△DCP；

(3)、当AB=5cm，AC=12cm时，求线段PC的长．

查看试题解析