安徽省黄山市休宁县2021-2022学年九年级上学期第二次月考数学试题

试卷更新日期：2021-12-29 类型：月考试卷

进入出卷网下载

一、单选题

1. 抛物线 $y = {(x - 2020)}^{2} + 2021$ 的顶点坐标是（）

A、 $(- 2020 ， 2021)$ B、 $(2020 ， 2021)$ C、 $(2020 ， - 2021)$ D、 $(- 2020 ， - 2021)$

查看试题解析
2. 已知 $\sqrt{3}$ 是方程x²﹣3 $\sqrt{3}$ x+c＝0的一个根，则c的值是（）

A、﹣6 B、6 C、 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
3. 为了解学生假期每天帮忙家长做家务活动情况，学校团委随机抽取了部分学生进行线上调查，并将调查结果绘制成频数直方图（不完整，每组含最小值，不含最大值），并且知道80～100分钟占所抽查学生的17.5%，根据提供信息，以下说法错误的是（）

A、本次共随机抽取了40名学生； B、抽取学生中每天做家务时间的中位数落在40～60分钟这一组； C、如果全校有800名学生，那么每天做家务时间超过1小时的大约有300人； D、扇形统计图中0～20分钟这一组的扇形圆心角的度数是30°；

查看试题解析
4. 抛物线y＝2x²与y＝－2x²相同的性质是（）

A、开口向下 B、对称轴是y轴 C、有最低点 D、对称轴是x轴

查看试题解析
5. 某校高一年级今年计划招四个班的新生，并采取随机摇号的方法分班，小明和小红既是该校的高一新生，又是好朋友，那么小明和小红分在同一个班的机会是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
6. 如图，在⊙O中，弦AC∥半径OB，∠BOC＝48°，则∠OAB的度数为（）

A、24° B、30° C、50° D、60°

查看试题解析
7. $△ C O D$ 是 $△ A O B$ 绕点O顺时针方向旋转 $3 0^{°}$ 后所得的图形，点C恰好在 $A B$ 上，则 $∠ A$ 的度数为（）

A、 $3 0^{°}$ B、 $6 0^{°}$ C、 $7 0^{°}$ D、 $7 5^{°}$

查看试题解析
8. 若二次函数 $y = x^{2} + m x$ 的对称轴是x=4，则关于x的方程 $x^{2} + m x = 9$ 的解为（　　）

A、x₁=0，x₂=8 B、x₁=1，x₂=9 C、x₁=1，x₂=﹣9 D、x₁=﹣1，x₂=9

查看试题解析
9. 已知等腰三角形的两边长分别是一元二次方程 $x^{2} - 6 x + 8 = 0$ 的两根，则该等腰三角形的底边长为（）

A、2 B、4 C、8 D、2或4

查看试题解析
10. 如图，二次函数y＝ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为（ $\frac{1}{2}$ ， 1），下列结论：①abc＜0；②b²﹣4ac＞0；③a+b＜0；④2a+c＜0，其中正确的个数是（　　）

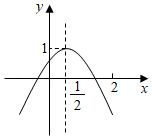A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 点（1，2）关于原点的对称点的坐标为．

查看试题解析
12. 如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则BH的长度为．

查看试题解析
13. 若一个圆锥的母线长为4，底面半径是1，则它的侧面展开图的面积是．

查看试题解析
14. 我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长，进而确定圆周率．某圆的半径为R，其内接正十二边形的周长为C．若R＝ $\sqrt{6} + \sqrt{2}$ ，则C＝， $\frac{C}{2 R}$ ≈（结果精确到0.01，参考数据： $\sqrt{6}$ ≈2.449， $\sqrt{2}$ ≈1.414）．

查看试题解析

三、解答题

15. 解方程： $3 x (x + 1) = 3 x + 3$ ．

查看试题解析
16. 某汽车专卖店经销某种型号的汽车．已知该型号汽车的进价为15万元/辆，经销一段时间后发现：当该型号汽车售价定为25万元/辆时，平均每周售出8辆；售价每降低0.5万元，平均每周多售出1辆．

(1)、当售价为22万元/辆时，求平均每周的销售利润．

(2)、若该店计划平均每周的销售利润是90万元，为了尽快减少库存，求每辆汽车的售价．

查看试题解析
17. 如图，在平面直角坐标系中，ΔABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，5）．

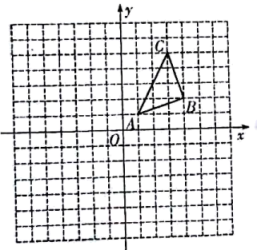
（1）请画出△ABC关于x轴的对称图形ΔA₁B₁C₁；
（2）借助网格，利用无刻度直尺画出线段CD，使CD平分ΔABC的面积．（保留确定点D的痕迹）．

查看试题解析
18. 如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．

(1)、求证：直线CD为⊙O的切线；

(2)、当AB＝2BE，且CE＝ $\sqrt{3}$ 时，求AD的长．

查看试题解析
19. 小明同学在探究如何计算连续正整数之和后，得到公式S（n）＝1＋2＋3＋…＋n＝ $\frac{n (n + 1)}{2}$ ，于是他猜想连续正整数的平方和S（n²）是否也有类似的公式，为此，他将相关数值列成如下表格，请观察表格规律，并完成问题：
n
1
2
3
4
5
6
…
S（n）
1
3
6
10
15
a
…
S（n²）
1
5
14
b
55
91
…
$\frac{S （ n^{2} ）}{S (n)}$
1
$\frac{5}{3}$
$\frac{7}{3}$
c
$\frac{11}{3}$
d
…

(1)、根据规律，表格中a＝；c＝；

(2)、用含n的代数式表示 $\frac{S （ n^{2} ）}{S (n)} =$ ；

(3)、推导出计算公式S（n²）．

查看试题解析
20. 转转盘和摸球是等可能概率下的经典模型．

(1)、在一个不透明的口袋中，放入除颜色外其余都相同的4个小球，其中1个白球，3个黑球搅匀后，随机同时摸出2个球，求摸出两个都是黑球的概率(要求采用树状图或列表法求解)；

(2)、如图，转盘的白色扇形和黑色扇形的圆心角分别为120°和240°．让转盘自由转动2次，求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解)．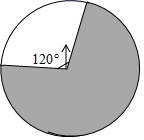

查看试题解析
21. 小红经营的网店以销售文具为主，其中一款笔记本进价为10元/本，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量y（单位：本）与线下售价x（单位：元/本， $12 \leq x \leq 16$ ，且x为整数）满足一次函数的关系，部分数据如下表：

x（元/本）

12

13

14

15

16

y（本）

120

110

100

90

80

(1)、求y与x的函数关系式；

(2)、若线上售价始终比线下每本便宜1元，且线上的月销量固定为40件．试问：当x为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．

查看试题解析
22. 如图1，在△ABC中，AB＝AC，∠BAC＝α，点D、E分别在边AB、AC上，AD＝AE，连接DC，点F、P、G分别为DE、DC、BC的中点．

(1)、观察猜想：图1中，线段PF与PG的数量关系是， ∠FPG＝（用含α的代数式表示）

(2)、探究证明：当△ADE绕点A旋转到如图2所示的位置时，小新猜想（1）中的结论仍然成立，请你证明小新的猜想．

查看试题解析
23. 如图，抛物线y=ax² + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1，已知：A(-1，0)、C(0，-3)．

(1)、求抛物线y= ax² + bx + c 的解析式；

(2)、求△AOC和△BOC的面积比；

(3)、在对称轴上是否存在一个P点，使△PAC的周长最小．若存在，请你求出点P的坐标；若不存在，请你说明理由．

查看试题解析

n	1	2	3	4	5	6	…
S（n）	1	3	6	10	15	a	…
S（n²）	1	5	14	b	55	91	…
$\frac{S （ n^{2} ）}{S (n)}$	1	$\frac{5}{3}$	$\frac{7}{3}$	c	$\frac{11}{3}$	d	…

x（元/本）	12	13	14	15	16
y（本）	120	110	100	90	80