安徽省淮北市五校联考2021-2022学年上学期九年级第三次月考数学试题
试卷更新日期:2021-12-29 类型:月考试卷
一、单选题
-
1. 已知x:y=5:2,则下列各式中错误的是( )A、 B、 C、 D、2. 如图,学校旁边一处斜坡OA上有一棵风景树,树高BC为6.5米,903班数学活动小组在某个时刻测得树的影长CD为2.5米,此时阳光恰好垂直照射在斜坡上,则这个斜坡的坡度为( )
 A、1:2.6 B、1:2.4 C、12:13 D、13:123. 反比例函数y=的图象的两个分支上,y都随x的增大而减小,则k的取值范围是( )A、k<3 B、k>0 C、k>3 D、k<04. 抛物线y=x+2先向右平移2个单位,再向下平移5个单位得到的抛物线的表达式是( )A、y=(x-2)+7 B、y=(x-2)-3 C、y=(x-5)+4 D、y=(x+2)-35.
A、1:2.6 B、1:2.4 C、12:13 D、13:123. 反比例函数y=的图象的两个分支上,y都随x的增大而减小,则k的取值范围是( )A、k<3 B、k>0 C、k>3 D、k<04. 抛物线y=x+2先向右平移2个单位,再向下平移5个单位得到的抛物线的表达式是( )A、y=(x-2)+7 B、y=(x-2)-3 C、y=(x-5)+4 D、y=(x+2)-35.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()
 A、(2,3) B、(3,2) C、(3,3) D、(4,3)6. 如果两个相似三角形的面积比是4:9,则它们对应边上的高之比为( )A、4:9 B、16:81 C、2:3 D、3:27. 在4×4网格中,∠α的位置如图所示,则sinα的值为( )
A、(2,3) B、(3,2) C、(3,3) D、(4,3)6. 如果两个相似三角形的面积比是4:9,则它们对应边上的高之比为( )A、4:9 B、16:81 C、2:3 D、3:27. 在4×4网格中,∠α的位置如图所示,则sinα的值为( ) A、 B、 C、2 D、8. 如图,点D在的边上,添加下列一个条件仍不能判断与相似的是( )
A、 B、 C、2 D、8. 如图,点D在的边上,添加下列一个条件仍不能判断与相似的是( ) A、 B、 C、 D、9. 二次函数y=ax+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,下列结论:①ac>0;②2a+b=0;③b-4ac>0;④a-b+c>0;其中正确的是( )
A、 B、 C、 D、9. 二次函数y=ax+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,下列结论:①ac>0;②2a+b=0;③b-4ac>0;④a-b+c>0;其中正确的是( )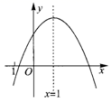 A、①② B、②③ C、②③④ D、①②③④10. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
A、①② B、②③ C、②③④ D、①②③④10. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( ) A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或二、填空题
-
11. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为m
 12. 如图,点A在双曲线y=上,点B在双曲线y=上,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为
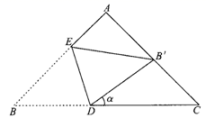
12. 如图,点A在双曲线y=上,点B在双曲线y=上,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为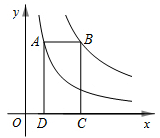 13. 如图,在四边形ABCD中,∠A=∠D=120°,AB=6、AD=4,点E、F分别在线段AD、DC上(点E与点A、D不重合),若∠BEF=120°,AE=x、DF=y,则y关于x的函数关系式为
13. 如图,在四边形ABCD中,∠A=∠D=120°,AB=6、AD=4,点E、F分别在线段AD、DC上(点E与点A、D不重合),若∠BEF=120°,AE=x、DF=y,则y关于x的函数关系式为 14. 某电商平台11月1日起开始销售一款新品牌手机,当月的日销售额y(万元)和销售时间第x天(1≤x≤30且x为整数)之间满足二次函数关系y=-(x-h)+k,根据市场调查可以确定在当月中旬日销售额达到最大值.(1)、若第18天的销售额比第19天的销售额多5万元,则第天的日销售额最大;(2)、若第18天后的日销售额呈下降趋势,则h的取值范围是
14. 某电商平台11月1日起开始销售一款新品牌手机,当月的日销售额y(万元)和销售时间第x天(1≤x≤30且x为整数)之间满足二次函数关系y=-(x-h)+k,根据市场调查可以确定在当月中旬日销售额达到最大值.(1)、若第18天的销售额比第19天的销售额多5万元,则第天的日销售额最大;(2)、若第18天后的日销售额呈下降趋势,则h的取值范围是三、解答题
-
15. 计算:16. 如图,已知AE为∠BAC的平分线,ED∥CA,若BE=2、EC=3、AC=4,求AD的长.
 17. 如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题.
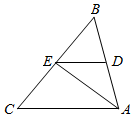
17. 如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题. (1)、以图中的点O为位似中心,将△ABC作位似变换放大到原来的两倍,得到ΔA1B1C1;(2)、若△ABC内一点P的坐标为(a,b),则位似变换后对应的点P'的坐标是;18. 如图,直线y=k1x+b与双曲线y=相交于A(1,2)、B(m,-1)两点.
(1)、以图中的点O为位似中心,将△ABC作位似变换放大到原来的两倍,得到ΔA1B1C1;(2)、若△ABC内一点P的坐标为(a,b),则位似变换后对应的点P'的坐标是;18. 如图,直线y=k1x+b与双曲线y=相交于A(1,2)、B(m,-1)两点. (1)、求直线和双曲线的函数表达式;(2)、观察图象,请直接写出不等式k1x+b>的解集;19. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
(1)、求直线和双曲线的函数表达式;(2)、观察图象,请直接写出不等式k1x+b>的解集;19. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.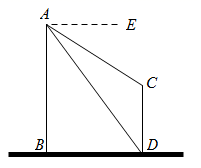 (1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)20. 如图,在▱ABCD中,点E、F分别是边AD和对角线AC上的点,连接EF,且∠AEF =∠CAB
(1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)20. 如图,在▱ABCD中,点E、F分别是边AD和对角线AC上的点,连接EF,且∠AEF =∠CAB (1)、求证:ΔAEF∽ΔACD;(2)、若AF=2CF,AE=4、DE=5,求AC的长.21. 如图,直线y=x+b和抛物线y=axx+2都经过A(0,n)和B(m,4)两点,抛物线y=axx+2与x轴交于C、D两点(点C在点D右侧)
(1)、求证:ΔAEF∽ΔACD;(2)、若AF=2CF,AE=4、DE=5,求AC的长.21. 如图,直线y=x+b和抛物线y=axx+2都经过A(0,n)和B(m,4)两点,抛物线y=axx+2与x轴交于C、D两点(点C在点D右侧)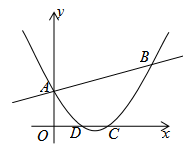 (1)、求直线和抛物线的函数表达式;(2)、求四边形ABCD的面积S;(3)、在x轴上是否存在点P,使得ΔPAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
(1)、求直线和抛物线的函数表达式;(2)、求四边形ABCD的面积S;(3)、在x轴上是否存在点P,使得ΔPAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.