安徽省淮北市名校联考2021-2022学年九年级上学期第三次月考数学试题
试卷更新日期:2021-12-29 类型:月考试卷
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、3. 二次函数y=x2﹣1的图象可由下列哪个函数图象向右平移1个单位,向下平移2个单位得到( )A、y= +1 B、y= +1 C、y= ﹣3 D、y= +34. 若线段AB=4,点Р是线段AB的黄金分割点,则线段AP的长是( )A、 B、 C、或 D、或5. 下面四组图形中,必是相似三角形的为( )A、两个直角三角形 B、两条边对应成比例,一个对应角相等的两个三角形 C、有一个角为40°的两个等腰三角形 D、有一个角为100°的两个等腰三角形6. 已知A、B两点的坐标分别为(-6,3)、(-12,8),ABO与是以原点О为位似中心的位似图形,若点的坐标为(2,-1),则点的坐标为( )A、(-4,) B、(4,-) C、(-6,4) D、(6,-4)7. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
2. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、3. 二次函数y=x2﹣1的图象可由下列哪个函数图象向右平移1个单位,向下平移2个单位得到( )A、y= +1 B、y= +1 C、y= ﹣3 D、y= +34. 若线段AB=4,点Р是线段AB的黄金分割点,则线段AP的长是( )A、 B、 C、或 D、或5. 下面四组图形中,必是相似三角形的为( )A、两个直角三角形 B、两条边对应成比例,一个对应角相等的两个三角形 C、有一个角为40°的两个等腰三角形 D、有一个角为100°的两个等腰三角形6. 已知A、B两点的坐标分别为(-6,3)、(-12,8),ABO与是以原点О为位似中心的位似图形,若点的坐标为(2,-1),则点的坐标为( )A、(-4,) B、(4,-) C、(-6,4) D、(6,-4)7. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有 A、1条 B、2条 C、3条 D、4条8. 在ABC中, ,则ABC一定是( )A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形9. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°10. 如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为( )
A、1条 B、2条 C、3条 D、4条8. 在ABC中, ,则ABC一定是( )A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形9. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°10. 如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为( ) A、
A、 B、
B、 C、
C、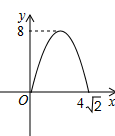 D、
D、
二、填空题
-
11. 若是关于x的二次函数,则m= .12. 如图,点A在反比例函数(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则k的值为 .
 13. 如图,两个宽度都为1的平直纸条,交叉叠放在一起,两纸条边缘的夹角为=30°,则它们重叠部分(图中阴影部分)的面积为 .
13. 如图,两个宽度都为1的平直纸条,交叉叠放在一起,两纸条边缘的夹角为=30°,则它们重叠部分(图中阴影部分)的面积为 .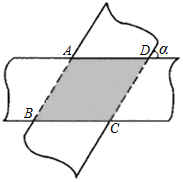 14. 如图,已知点E是矩形的对角线上的一动点,正方形的顶点都在边上,若 , 则 .
14. 如图,已知点E是矩形的对角线上的一动点,正方形的顶点都在边上,若 , 则 .
三、解答题
-
15. 用配方法求二次函数的顶点坐标.16. 计算:17. 已知二次函数解析式为(m是常数).(1)、求证:不论m为何值,函数图象与x轴总是没有公共点;(2)、把该函数图象沿平行y轴方向怎样平移,得到的图象与x轴只有一个交点?18. 已知P(-3,m)和Q(1,m)是抛物线上的两点.(1)、求b的值;(2)、判断关于x的一元二次方程是否有实数根,若有求出实数根;若没有请说明理由.19. 如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
 (1)、请写出图中各对相似三角形(相似比为1除外);(2)、求BP:PQ:QR.20. 淮北市为缓解“停车难”问题.建造地下停车库,如图已知 , , C在BD上, . 根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶员能否安全驶入.小明认为CD的长就是限高值,而小亮认为应该以CE的长作为限高值.(参考数据: , , , 结果精确到)
(1)、请写出图中各对相似三角形(相似比为1除外);(2)、求BP:PQ:QR.20. 淮北市为缓解“停车难”问题.建造地下停车库,如图已知 , , C在BD上, . 根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶员能否安全驶入.小明认为CD的长就是限高值,而小亮认为应该以CE的长作为限高值.(参考数据: , , , 结果精确到)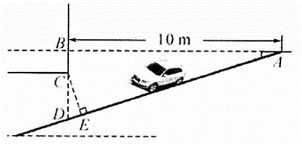 (1)、请你判断小明和小亮谁说的对?(2)、计算出正确的限高值.21. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75.其图象如图.
(1)、请你判断小明和小亮谁说的对?(2)、计算出正确的限高值.21. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75.其图象如图. (1)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元;(2)、销售单价在什么范围时,该种商品每天的销售利润不低于16元.22. 如图1,E是等边ABC的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边AEF,连接CF.已知ECF的面积(S)与BE的长(x)之间的函数关系如图2所示(P为抛物线的顶点)﹒
(1)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元;(2)、销售单价在什么范围时,该种商品每天的销售利润不低于16元.22. 如图1,E是等边ABC的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边AEF,连接CF.已知ECF的面积(S)与BE的长(x)之间的函数关系如图2所示(P为抛物线的顶点)﹒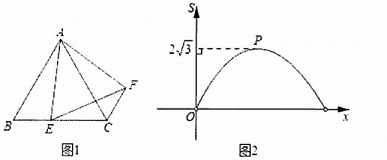 (1)、当ECF的面积最大时,求∠FEC的度数;(2)、求等边ABC的边长.23. 如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至 , 旋转角为.
(1)、当ECF的面积最大时,求∠FEC的度数;(2)、求等边ABC的边长.23. 如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至 , 旋转角为. (1)、当点D′恰好落在EF边上时,求旋转角的值;(2)、如图2,G为BC的中点,且0°<<90°,求证:;(3)、小长方形CEFD绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
(1)、当点D′恰好落在EF边上时,求旋转角的值;(2)、如图2,G为BC的中点,且0°<<90°,求证:;(3)、小长方形CEFD绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.