安徽省淮北市五校联考2021-2022学年八年级上学期第三次月考数学试题

试卷更新日期：2021-12-29 类型：月考试卷

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若点P的坐标为（−3，2022），则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知一个三角形的两条边长分别为4和7，则第三条边的长度不能是（）

A、11 B、9 C、8 D、7

查看试题解析
4. 将一次函数 $y = - 2 x$ 的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为（）

A、 $y = - 2 (x - 4)$ B、 $y = - 2 x + 4$ C、 $y = - 2 (x + 4)$ D、 $y = - 2 x - 4$

查看试题解析
5. 如图，点B，C在线段AD上，AB＝CD，AE∥BF，添加一个条件仍不能判定△AEC≌△BFD的是（）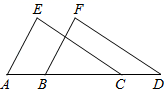

A、AE＝BF B、CE＝DF C、∠ACE＝∠BDF D、∠E＝∠F

查看试题解析
6. 如果一个三角形的两个内角都小于30°，那么这个三角形的形状是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
7. 如图，AB∥CD，AD∥BC，AC与BD相交于点O，AE⊥BD，CF⊥AC，垂足分别是E，F．则图中共有（）对全等三角形．

A、5 B、6 C、7 D、8

查看试题解析
8. 一次函数 $y = - m x + m$ 与正比例函数 $y = m x$ （m是常数，且 $m \neq 0$ ）在同一平面直角坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析
9. 如图，∠C=90°，AD平分∠BAC，DE⊥AB于点E，有下列结论：①CD=ED ；②AC+ BE= AB ；③DA平分∠CDE ；④∠BDE =∠BAC；⑤ $S_{Δ A B D} ： S_{Δ A C D}$ =AB：AC，其中结论正确的个数有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
10. 在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，图中的折线段表示甲、乙两车之间的距离y（千米）与行驶时间x（小时）的函数关系的图象，下列说法错误的是（）

A、乙先出发的时间为0.5小时 B、甲的速度是80千米/小时 C、甲出发0.5小时后两车相遇 D、甲到B地比乙到A地早 $\frac{1}{12}$ 小时

查看试题解析

二、填空题

11. 正方形的对称轴的条数为．

查看试题解析
12. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，若AB=4，CF=3，则BD= ．

查看试题解析
13. 已知点A(a，0)和点B(0，5)两点，且直线AB与坐标轴围成的三角形的面积等于10，则a的值是.

查看试题解析
14. 已知一次函数y=3x+4−2a．

(1)、若该函数图象与y轴的交点位于y轴的负半轴，则a的取值范围是；

(2)、当−2≤x≤3时，函数y有最大值-4，则a的值为．

查看试题解析

三、解答题

15. 在△ABC中，∠B＝20°＋∠A，∠C＝∠B－10°，求∠A的度数．

查看试题解析
16. 如图，在边长为1个单位长度的10×8小正方形网格中，给出了以格点（网格线的交点）为顶点的△ABC，点A，C的坐标分别为（−3，2），（−1，3），直线l在网格线上．

(1)、建立平面直角坐标系，画出△ABC关于直线l对称的△A₁B₁C₁；（点A₁ ， B₁ ， C₁分别为点A，B，C的对应点）

(2)、若点P（a，b）是△ABC内任意一点，其关于直线l的对称点是P₁ ，则点P₁的坐标是．

查看试题解析
17. 已知正比例函数的图象经过点（3，−6）．

(1)、求这个函数的解析式：

(2)、图象上有两点B（x₁ ， y₁）、C（x₂ ， y₂），如果 $x_{1} > x_{2}$ ，比较 $y_{1}$ ， $y_{2}$ 的大小．

查看试题解析
18. 课间，小明拿着老师的等腰三角板玩，不小心掉在两墙之间，如图所示：

(1)、求证：△ADC≌△CEB；

(2)、已知DE=35cm，请你帮小明求出砌墙砖块的厚度a的大小（每块砖的厚度相同）

查看试题解析
19. 如图，在 $△ A B C$ 中AD是BC边上的中线， $A B ∥ C E$ ，过C作AB的平行线交AD的延长线于E点．

(1)、求证： $A B = E C$ ；

(2)、若 $A B = 6$ ， $A C = 2$ ，试求中线AD的取值范围．

查看试题解析
20. 如图，已知直线l的解析式为y=x+4，它与y轴交于点A，与x轴交于点B．

(1)、写出A，B两点的坐标；

(2)、若点C坐标为（−2，0），请在直线l上找一点P，使得OP+CP的值最小，求点P的坐标．

查看试题解析
21. 如图1，已知A，E，F，C在同一条直线，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，AB=CD．

(1)、求证：DB平分EF；

(2)、若△DEC的边EC沿AC方向移动，其余条件不变，如图2，上述结论是否仍成立？请说明理由．

查看试题解析
22. 如图，直线l：y＝﹣ $\frac{1}{3}$ x+2与x轴、y轴分别交于A、B两点，动点M从点A以每秒1个单位的速度沿x轴向左移动.

(1)、求A、B两点的坐标；

(2)、将直线l向上平移4个单位后得到直线l'，交y轴于点C.求直线l′的函数表达式；

(3)、设点M的移动时间为t，当t为何值时，△COM≌△AOB，并求出此时点M的坐标.

查看试题解析
23. 如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．

(1)、求证：AE＝CD；

(2)、求证：AE⊥CD；

(3)、连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD，其中正确的一个是（请写序号），并给出证明过程．

查看试题解析