2021-2022学年度第一学期九年级数学第21--24章 期末综合复习练习卷(人教版)
试卷更新日期:2021-12-29 类型:复习试卷
一、单选题
-
1. 二次函数 的图象是( )A、
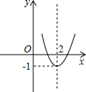 B、
B、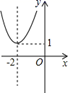 C、
C、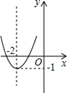 D、
D、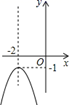 2. 如果将抛物线y=x2﹣4x﹣1平移,使它与抛物线y=x2﹣1重合,那么平移的方式可以是( )A、向左平移2个单位,向上平移4个单位 B、向左平移2个单位,向下平移4个单位 C、向右平移2个单位,向上平移4个单位 D、向右平移2个单位,向下平移4个单位3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
2. 如果将抛物线y=x2﹣4x﹣1平移,使它与抛物线y=x2﹣1重合,那么平移的方式可以是( )A、向左平移2个单位,向上平移4个单位 B、向左平移2个单位,向下平移4个单位 C、向右平移2个单位,向上平移4个单位 D、向右平移2个单位,向下平移4个单位3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 将点A(﹣3,4)绕原点顺时针方向旋转180°后得到点B,则点B的坐标为( )A、(3,﹣4) B、(﹣4,3) C、(﹣4,﹣3) D、(﹣3,﹣4)5. 已知直线l及直线l外一点P.如图,(1)在直线l上取一点O,以点O为圆心,OP长为半径画半圆,交直线l于A,B两点;(2)连接PA,以点B为圆心,AP长为半径画弧,交半圆于点Q;(3)作直线PQ,连接BP.根据以上作图过程及所作图形,下列结论中错误的是( )
4. 将点A(﹣3,4)绕原点顺时针方向旋转180°后得到点B,则点B的坐标为( )A、(3,﹣4) B、(﹣4,3) C、(﹣4,﹣3) D、(﹣3,﹣4)5. 已知直线l及直线l外一点P.如图,(1)在直线l上取一点O,以点O为圆心,OP长为半径画半圆,交直线l于A,B两点;(2)连接PA,以点B为圆心,AP长为半径画弧,交半圆于点Q;(3)作直线PQ,连接BP.根据以上作图过程及所作图形,下列结论中错误的是( ) A、AP=BQ B、PQ∥AB C、∠ABP=∠PBQ D、∠APQ+∠ABQ=180°6. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )
A、AP=BQ B、PQ∥AB C、∠ABP=∠PBQ D、∠APQ+∠ABQ=180°6. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )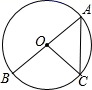 A、 B、 C、 D、7. 已知二次函数 的图象如图,则下列结论中正确的是( )
A、 B、 C、 D、7. 已知二次函数 的图象如图,则下列结论中正确的是( )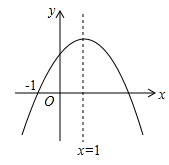 A、 B、 C、 D、 的符号无法确定8. 抛物线 向左平移5个单位,再向下平移1个单位,所得到的抛物线是( )A、 B、 C、 D、9. 如图,平面直角坐标系中,抛物线y= x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A、 B、 C、 D、 的符号无法确定8. 抛物线 向左平移5个单位,再向下平移1个单位,所得到的抛物线是( )A、 B、 C、 D、9. 如图,平面直角坐标系中,抛物线y= x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )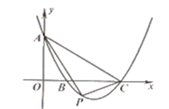 A、
A、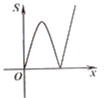 B、
B、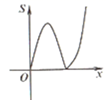 C、
C、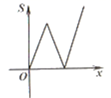 D、
D、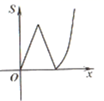 10. 已知二次函数y=(m﹣2)x2+2mx+m﹣3的图象与x轴有两个交点,(x1 , 0),(x2 , 0),则下列说法正确是( )
10. 已知二次函数y=(m﹣2)x2+2mx+m﹣3的图象与x轴有两个交点,(x1 , 0),(x2 , 0),则下列说法正确是( )①该函数图象一定过定点(﹣1,﹣5);②若该函数图象开口向下,则m的取值范围为: m<2;③当m>2,且1≤x≤2时,y的最大值为:4m﹣5;④当m>2,且该函数图象与x轴两交点的横坐标x1 , x2满足﹣3<x1<﹣2,﹣1<x2<0时,m的取值范围为: m<11.
A、①②③④ B、①②④ C、①③④ D、②③④二、填空题
-
11. 二次函数 的图象开口方向是(填“向上”或“向下”).12. 一元二次方程 的根是.13. 圆锥的侧面展开图是一个弧长为6π的扇形,则这个圆锥底面半径是.14. 一条弦分圆为7:5两部分,这条弦所对的圆周角的度数.15. 如图, 为 的直径,C为 上一动点,将 绕点A逆时针旋转120°得 ,若 ,则 的最大值为.

三、解答题
-
16. 抛物线的顶点为 ,且过点 ,求它的函数解析式.17. 如图,直径为 的圆柱形水管有积水(阴影部分),水面的宽度 为 ,求水的最大深度 .
 18. 已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD .
18. 已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD . 19. 如图,一个边长为 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 中,点G、E、F分别在 、 、 上,且 .在 、 、五边形 三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.问:点E在什么位置时,正方形花坛种植花卉所需的总费用最少,最少为多少元?
19. 如图,一个边长为 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 中,点G、E、F分别在 、 、 上,且 .在 、 、五边形 三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.问:点E在什么位置时,正方形花坛种植花卉所需的总费用最少,最少为多少元? 20. 如图,在 中,直径 与弦 相交于点 , .
20. 如图,在 中,直径 与弦 相交于点 , .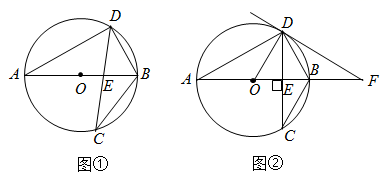
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点 作 的切线 ,与 的延长线相交于点 .求 的大小.
21. 某旅游园区对团队入园购票规定:如团队人数不超过 人,那么这个团队需交200元入园费;若团队人数超过 人,则这个团队除了需交200元入园费外,超过部分游客还要按每人 元交入园费,下表是两个旅游团队人数和入园缴费情况:旅游团队名称
团队人数(人)
入园费用(元)
旅游团队1
80
350
旅游团队2
45
200
根据上表的数据,求某旅游园区对团队入园购票规定的 人是多少?
四、综合题
-
22. 某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,分析得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1= x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.(1)、试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售间x(天)之间的函数关系式;(2)、请问在这30天的销售期中,哪一天的日销售利润最大?请求出这个最大利润值是多少?(注:销售利润=销售收入-购进成本)