2021-2022学年度第一学期九年级数学第24章《圆》24.2点和圆、直线和圆的关系 期末复习练习卷（人教版）
试卷更新日期：2021-12-29 类型：复习试卷
一、单选题
-
1. Rt△ABC中，∠C=90°，AC=2，BC=4，如果以点为圆心，AC为半径作⊙A，那么斜边AB的中点D与⊙A的位置关系是（ ）．A、点D在⊙A外 B、点D在⊙A上 C、点D在⊙A内 D、无法确定2. 下列语句中，一定正确的是（ ）
①过三点有且只有一个圆；②平分弦的直径垂直于弦；③三角形的外心到三角形三个顶点的距离相等；④同弧或等弧所对的圆周角相等；⑤圆内接平行四边形是矩形．
A、①②③ B、①②④ C、②③⑤ D、③④⑤3. 已知矩形ABCD的边AB=15，BC=20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是（ ）.A、r＞15 B、15＜r＜20 C、15＜r＜25 D、20＜r＜254. 已知O是 的外心，连接AO并延长交BC于D， ，过D作 于E，若 ，则AC的长为（ ）
A、3 B、4 C、5 D、65. 如图，在 中， ∠ACB=90°， cm， cm. 是 边上的一个动点，连接 ，过点 作 于 ，连接 ，在点 变化的过程中，线段 的最小值是（ ）
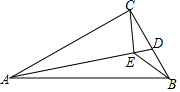A、1 B、 C、2 D、6. ⊙O的半径为6cm，圆心O到直线l的距离为7cm，则直线l与⊙O的位置关系是（ ）A、相交 B、相切 C、相离 D、不能确定7. 如图，P为半径是3的圆O外一点，PA切圆O于A，若AP＝4，则OP＝（ ）
A、2 B、3 C、4 D、58. 如图，在 APBC中，∠C=40°，若⊙O与PA，PB相切于点A，B，则∠CAB=（ ）
A、40° B、50° C、60° D、70°9. 如图，点O是△ABC的内切圆的圆心，若∠BAC＝80°，则∠BOC＝（ ）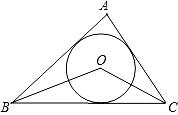
A、130° B、100° C、50° D、65°10. 如图，AB是⊙O的弦，作OC⊥OA交⊙O的切线BC于点C ， 交AB于点D ． 已知∠OAB＝20°，则∠OCB的度数为（ ）
A、20° B、30° C、40° D、50°二、填空题
-
11. 已知 的半径为10，直线AB与 相交，则圆心O到直线AB距离d的取值范围是 ．12. 如图，已知圆O为 的内切圆，切点分别为D、E、F，且 ， ， ，则圆O的半径为 ．
13. 如图， 是 的切线，切点为 是 的直径， 交 于点 ，连接 ，若 ，则 的度数为 ．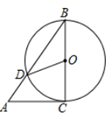
14. 在Rt ABC中，∠C=90°，AC=9，BC=12，则它的外接圆的半径为15. 如图，在平面直角坐标系中，A（0，4），B（4，4），C（6，2）．
（Ⅰ）若经过A、B、C三点的圆弧所在圆的圆心为M ，
点M的坐标为 ；⊙M的半径为 ；
（Ⅱ）若画出该圆弧所在圆，则在整个平面直角坐标系网格中该圆共经过 个格点．
三、解答题
-
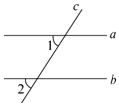
16. 已知：如图，直线a ， b被c所截，∠1，∠2是同位角，且∠1≠∠2．
求证：a不平行于b ．
17. 阅读下列文字，回答问题.题目：在Rt△ABC中，∠C=90°，若∠A≠45°，所以AC≠BC．
证明：假设AC=BC，∵∠A≠45°，∠C=90°，∴∠A≠∠B，∴AC≠BC．这与假设矛盾，所以AC≠BC．
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正.
18. 平面上有8条直线两两相交．试证明在所有的交角中至少有一个角小于23°．
19. 如图， 内接于 ，且 为 的直径，过点 作 的切线 交 的延长线于点 ，点 在直径 上，且 ，连接 并延长交 于点 .连接 ， ，试判断 与 的数量关系，并说明理由．
