2021-2022学年度第一学期九年级数学第24章《圆》24.1圆的有关性质 期末复习练习卷(人教版)
试卷更新日期:2021-12-29 类型:复习试卷
一、单选题
-
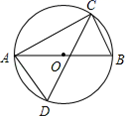
1. 如图,四边形ABCD内接于 ,如果它的一个外角 ,那么 的度数为( )
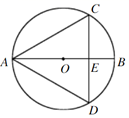
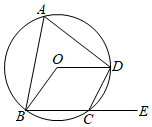 A、64° B、128° C、20° D、116°2. 如图所示,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
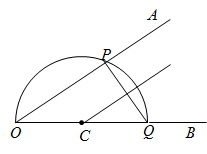
A、64° B、128° C、20° D、116°2. 如图所示,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A、12个单位 B、10个单位 C、1个单位 D、15个单位3. 下列图形中的角是圆周角的是( )A、
A、12个单位 B、10个单位 C、1个单位 D、15个单位3. 下列图形中的角是圆周角的是( )A、 B、
B、 C、
C、 D、
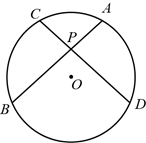
D、 4. 如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
4. 如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( ) A、82° B、38° C、24° D、41°5. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、146. 如图,AB是⊙O的直径,BC是弦,OD∥AC交 于点D,交BC于点E,若BC=8,ED=2,则⊙O的半径是( )
A、82° B、38° C、24° D、41°5. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、146. 如图,AB是⊙O的直径,BC是弦,OD∥AC交 于点D,交BC于点E,若BC=8,ED=2,则⊙O的半径是( ) A、3 B、4 C、5 D、27. 如图,在 中,半径 于点D, ,则下列说法正确的是( )
A、3 B、4 C、5 D、27. 如图,在 中,半径 于点D, ,则下列说法正确的是( )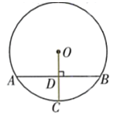 A、 B、 C、 D、AB垂直平分OC8. 如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( )
A、 B、 C、 D、AB垂直平分OC8. 如图,在半径为5的⊙ 中, , 是互相垂直的两条弦,垂足为 , ,则 的长为( ) A、3 B、4 C、 D、9. 如图,A、B,C是⊙O上的点,且∠ACB=140°.在这个图中,画出下列度数的圆周角:40°,50°,90°,140°,仅用无刻度的直尺能画出的有( )
A、3 B、4 C、 D、9. 如图,A、B,C是⊙O上的点,且∠ACB=140°.在这个图中,画出下列度数的圆周角:40°,50°,90°,140°,仅用无刻度的直尺能画出的有( )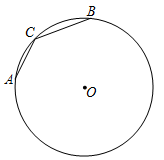 A、1个 B、2个 C、3个 D、4个10. 在 中,直径 弦 于点 若 ,则 的长为( )
A、1个 B、2个 C、3个 D、4个10. 在 中,直径 弦 于点 若 ,则 的长为( )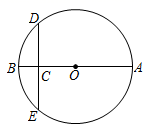 A、6 B、9 C、12 D、15
A、6 B、9 C、12 D、15二、填空题
-
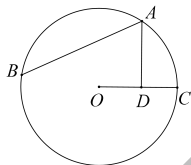
11. 如图,在⊙O中, =2 , 于点D,比较大小AB2AD.(填入“>”或“<”或“=”).
 12. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为 .
12. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为 . 13. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦, , , ,则弦AB和CD之间的距离是 .14. 如图, 为 的外接圆 的直径,若 ,则
13. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦, , , ,则弦AB和CD之间的距离是 .14. 如图, 为 的外接圆 的直径,若 ,则 15. 如图,在条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD且∠ACO=60°中,能推出四边形OCAD是菱形的条件有个.
15. 如图,在条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD且∠ACO=60°中,能推出四边形OCAD是菱形的条件有个.
三、解答题
-
16. 如图,在△ABC中AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,试求CD的长.
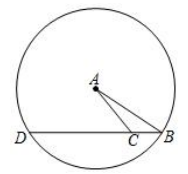 17. 如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,宽度为6米的船能否通过这座桥?请说明理由.
17. 如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,宽度为6米的船能否通过这座桥?请说明理由. 18. 已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.求证:AB=AC.
18. 已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.求证:AB=AC.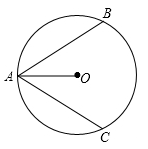 19. 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=68°,求∠BAC.
19. 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=68°,求∠BAC.