2021-2022学年度第一学期九年级数学第23章《旋转》23.2中心对称 期末复习练习卷(人教版)
试卷更新日期:2021-12-29 类型:复习试卷
一、单选题
-
1. 下列图形中一定是中心对称图形的是( )A、三角形 B、四边形 C、正五边形 D、平行四边形2. 随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,是中心对称图形但不是轴对称图形的是( ).A、
4. 下列图形中,是中心对称图形但不是轴对称图形的是( ).A、 B、
B、 C、
C、 D、
D、 5. 下面几种中式窗户图形既是轴对称又是中心对称的是( )A、
5. 下面几种中式窗户图形既是轴对称又是中心对称的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列图案中,是轴对称图形,但不是中心对称图形的是( )A、
6. 下列图案中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 若点P(2−m,5)关于原点对称的点是P'(3,2n+1),则m-n的值为( )A、6 B、-3 C、8 D、98. 已知点 和 关于原点对称,则 的值为( )A、1 B、-1 C、3 D、-39. 在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P的坐标是( )A、(3,1) B、(﹣3,﹣1) C、(﹣3,1) D、(﹣1,3)10. 点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )A、﹣3 B、﹣4 C、3 D、4
7. 若点P(2−m,5)关于原点对称的点是P'(3,2n+1),则m-n的值为( )A、6 B、-3 C、8 D、98. 已知点 和 关于原点对称,则 的值为( )A、1 B、-1 C、3 D、-39. 在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P的坐标是( )A、(3,1) B、(﹣3,﹣1) C、(﹣3,1) D、(﹣1,3)10. 点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )A、﹣3 B、﹣4 C、3 D、4二、填空题
-
11. 在平面直角坐标系中,点M(﹣2,4)关于原点对称的点的坐标是 .12. 如图,以正方形ABCD的中心O为原点建立平面直角坐标系,若点A的坐标为(-2,-2),则点 的坐标是 .
 13. 写出一个四边形,使它既是中心对称图形又是轴对称图形,则这个四边形可能是 .14. 在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:.15. 如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是.
13. 写出一个四边形,使它既是中心对称图形又是轴对称图形,则这个四边形可能是 .14. 在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:.15. 如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是.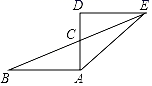
三、解答题
-
16. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .

⑴请画出 关于x轴对称的 ,并写出点 的坐标;
⑵以O为对称中心,画出 关于O成中心对称的图形 ;
⑶请用无刻度的直尺画出 的平分线 (点Q在线段 上)(保留作图辅助线).
17. 在如图所示的网格中建立平面直角坐标系, 的顶点在网格线的交点上,点 的坐标为 . (1)、画出 向上平移4个单位长度得到的 ,并写出点 的对应点 的坐标;(2)、画出 绕原点 顺时针旋转90°得到的 ,并写出点 的对应点 的坐标.18. 在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
(1)、画出 向上平移4个单位长度得到的 ,并写出点 的对应点 的坐标;(2)、画出 绕原点 顺时针旋转90°得到的 ,并写出点 的对应点 的坐标.18. 在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
⑴现将△ABC先向左平移5个单位长度,再向上平移2个单位长度,得到△A1B1C1 , 请在平面直角坐标系中画出△A1B1C1 .
⑵此时平移的距离是多少;
⑶在平面直角坐标系中画出△ABC关于点O成中心对称的△A2B2C2 .
19. 如图,线段AC,BD相交于点O,AB //CD, :A B=CD.线段AC上的两点E,F关于点O中心对称.求证:BF=DE.