2021-2022学年度第一学期九年级数学第21、22章期末综合复习练习卷（人教版）

试卷更新日期：2021-12-29 类型：复习试卷

进入出卷网下载

一、单选题

1. 将抛物线y＝（x﹣3）²﹣4向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）

A、y＝（x﹣4）²﹣6 B、y＝（x﹣2）²﹣2 C、y＝（x﹣1）²﹣3 D、y＝（x﹣4）²﹣2

查看试题解析
2. 已知四点 $A (0, - 2)$ ， $B (1, 0)$ ， $C (- 2, 0)$ ， $D (0, 4)$ ，若一个二次函数的图象经过这四点中的三点，则这个二次函数图象的对称轴为（）

A、 $x = \frac{1}{2}$ B、 $x = - 1$ C、 $x = 1$ D、 $x = - \frac{1}{2}$

查看试题解析
3. 关于二次函数 $y = x^{2}$ 图象，下列叙述正确的有（    ）
①它的图象是抛物线；    ②它的图象有最低点；

③它的图象经过 $(0 ， 0)$ ；    ④它的图象开口向上．

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 方程2x²+（k+1）x－6=0的两根和是－2，则k的值是（）

A、k=3 B、k=－ 3 C、k=0 D、k=1

查看试题解析
5. 若方程（a﹣3）x²＋x＋a＝0是关于x的一元二次方程，则（）

A、a≠0 B、a≠3 C、a＞0 D、a＞3

查看试题解析
6. 把抛物线 $y = x^{2} - 1$ 先向右平移2个单位，再向上平移2个单位，所得抛物线的解析式为（）

A、 $y = x^{2} + 8 x + 6$ B、 $y = x^{2} - 8 x + 6$ C、 $y = x^{2} - 4 x + 5$ D、 $y = x^{2} + 4 x + 5$

查看试题解析
7. 如图，抛物线y=ax²+bx+c（a>0）的对称轴是直线x=1，且经过点(3，0)，则a-b+c的值为（）

A、0 B、-1 C、 1 D、2

查看试题解析
8. 一元二次方程x²＝3x的解是（）

A、x＝3 B、x＝﹣3 C、x₁＝3，x₂＝0 D、x₁＝﹣3，x₂＝0

查看试题解析
9. 用配方法解方程时，下列配方错误的是（）．

A、 $x^{2} + 6 x - 7 = 0$ 化为 ${(x + 3)}^{2} = 0$ B、 $x^{2} - 5 x - 4 = 0$ 化为 ${(x - \frac{5}{2})}^{2} = \frac{41}{4}$ C、 $x^{2} + 2 x - 99 = 0$ 化为 ${(x + 1)}^{2} = 100$ D、 $3 x^{2} - 4 x - 2 = 0$ 化为 ${(x - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
10. 若关于x的一元二次方程 $(m - 3) x^{2} + 3 x + 1 = 0$ 有实数根，则m的取值范围中，正整数值有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

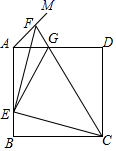
11. 二次函数 $y = x^{2} + 2 x + m$ 与坐标轴有两个不同的交点，则m的值为.

查看试题解析
12. 写出一个 $y$ 关于 $x$ 的函数关系式：满足在第一象限内， $y$ 随 $x$ 的增大而增大的函数是.

查看试题解析
13. 一元二次方程 $x^{2} - 4 x - 1 = 0$ 配方后可化为.

查看试题解析
14. 用配方法解一元二次方程 $x^{2} - 4 x = 5$ 时，此方程可变形为.

查看试题解析
15. 如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM＝45°，点F在射线AM上，且AF＝ $\sqrt{2}$ BE，CF与AD相交于点G，连接EC、EF、EG.则下列结论：①∠ECF＝45°；②△AEG的周长为（1+ $\frac{\sqrt{2}}{2}$ ）a；③BE²+DG²＝EG²；④△EAF的面积的最大值是 $\frac{1}{8}$ a²；⑤当时BE＝ $\frac{1}{3}$ a，G是线段AD的中点.其中正确的结论是.

查看试题解析

三、解答题

16. 已知抛物线的顶点坐标 $(1, 2)$ 且过点 $(3, 0)$ ，求该抛物线的解析式．

查看试题解析
17. 已知二次函数 $y = x^{2} + b x + c$ 的图象经过点 $A (1 ， 0) ， C (0 ， - 3)$ ，求此二次函数的解析式.

查看试题解析
18. 已知二次函数 $y = - x^{2} + b x + c$ 的图象经过 $(- 1, 0), (0, 5)$ 两点，求此二次函数的解析式.

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - (m + 3) x + m + 2 = 0$ .若方程有一个根的平方等于9，求m的值.

查看试题解析
20. 已知关于x的方程x²﹣2mx+3+4m²﹣6=0的两根为α，β，
试求（α﹣1）²+（β﹣1）²的最大值与最小值．

查看试题解析
21. 已知关于 $x$ 的方程 $x^{2} + (m + 2) x + 2 m - 1 = 0$ ，当 $m$ 为何值时，方程的两根相互为相反数？并求出此时方程的解.

查看试题解析
22. 已知a、b、c是等腰△ABC的三边长，其中a＝4，b和c是关于x的方程x²-mx+3m＝0的两根，求m的值．

查看试题解析

2021-2022学年度第一学期九年级数学第21、22章 期末综合复习练习卷（人教版）

一、单选题

二、填空题

三、解答题

2021-2022学年度第一学期九年级数学第21、22章期末综合复习练习卷（人教版）