2021-2022学年度第一学期九年级数学第22章《二次函数》22.3实际问题与一元二次方程 期末复习练习卷（人教版）

试卷更新日期：2021-12-29 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 某种商品的价格是 2 元，准备进行两次降价．如果每次降价的百分率都是 x ，经过两次降价后的价格 y （单位：元）随每次降价的百分率 x 的变化而变化，则 y 关于 x 的函数解析式是（    ）
    A、y=2(x+1)2 B、y=2(1−x)2 C、y=(x+1)2 D、y=(x−1)2

    查看试题解析

  • 2. 某店销售一款运动服，每件进价100元，若按每件128元出售，每天可卖出100件，根据市场调查结果，若每件降价1元，则每天可多卖出5件，要使每天获得的利润最大，则每件需要降价（    ）
    A、3元 B、4元 C、5元 D、8元

    查看试题解析

  • 3. 如图，若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）具有函数关系为 h=20t−5t2 ，则小球从飞出到落地的所用时间为 ( 　　 )

    A、3s B、4s C、5s D、6s

    查看试题解析

  • 4. 如图，函数 y=−x2+12 的图象与x轴交于A，B两点，点C是以 M(0 ， 2) 为圆心，2为半径的圆上的动点，P是 AC 的中点，连结 OP ，则线段 OP 的最小值是（    ）

    A、1 B、3 C、2 D、7

    查看试题解析

  • 5. 小杰把班级勤工俭学挣得的班费500元按一年期存入银行，已知年利率为x，一年到期后银行将本金和利息自动按一年定期转存，设两年到期后，本利和为y元，则y与x之间的函数关系式为（    ）
    A、y=500(x+1)2 B、y=x2+500 C、y=x2+500x D、y=x2+5x

    查看试题解析

  • 6. 某商品的进价为每件20元，现在的售价为每件40元，每星期可卖出200件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出5件．则每星期售出商品的利润y（单位：元）与每件涨价x（单位：元）之间的函数关系式是（    ）
    A、y＝（200﹣5x）（40﹣20＋x） B、y＝（200＋5x）（40﹣20﹣x） C、y＝200（40﹣20﹣x） D、y＝200﹣5x

    查看试题解析

  • 7. 某店销售一款运动服，每件进价100元，若按每件128元出售，每天可卖出100件，根据市场调查结果，若每件降价1元，则每天可多卖出5件，要使每天获得的利润最大，则每件需要降价（　　）元。
    A、3元 B、4元 C、5元 D、8元

    查看试题解析

  • 8. 某超市销售一种商品，每件成本为50元，销售人员经调查发现，该商品每月的销售量 y （件）与销售单价 x （元）之间满足函数关系式 y=−5x+550 ，若要求销售单价不得低于成本，为每月所获利润最大，该商品销售单价应定为多少元？每月最大利润是多少？（    ）
    A、90元，4500元 B、80元，4500元 C、90元，4000元 D、80元，4000元

    查看试题解析

  • 9. 如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m ， 则水面下降1m时，水面宽度增加（    ）

    A、1m B、2m C、（2 6 ﹣4）m D、（ 6 ﹣2）m

    查看试题解析

  • 10. 如图，以40m/s的速度将小球沿与地面成30°角的方向击出后，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h(单位：m)与飞行时间t(单位：s)之间具有函数关系h＝20t－5t2 ． 下列叙述正确的是( （   ）

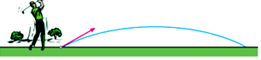    A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m  C、小球从飞出到落地要用时4s  D、小球飞出1s时的飞行高度为10m

    查看试题解析

二、填空题

  • 11. 一位运动员投掷铅球，如果铅球运行时离地面的高度为y（米）关于水平距离x（米）的函数解析式为y=﹣112x2×23x+53 ， 那么铅球运动过程中最高点离地面的距离为米．

    查看试题解析

  • 12. 退休的李老师借助自家15米的院墙和总长度为30米的围栏，在院墙外设计一个矩形花圃种植花草．为方便进出，他在如图所示的位置安装了一个1米宽的门，如果设和墙相邻的一边长为x米，花圃面积为y平方米，则y与x之间的函数关系式为 ．

    查看试题解析

  • 13. 如图，某学校拟建一块矩形花圃，打算一边利用学校现有的墙 （ 墙足够长 ） ，其余三边除门外用栅栏围成，栅栏总长度为50m，门宽2m.这个矩形花圃的最大面积是m2.

    查看试题解析

  • 14. 小王想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．则S与x之间的函数关系式是 ． （不用写自变量的取值范围）

    查看试题解析

  • 15. 如图，线段 AB=8 ，点 C 是 AB 上一点，点 D 、 E 是线段 AC 的三等分点，分别以 AD 、 DE 、 EC 、 CB 为边作正方形，则 AC= 时，四个正方形的面积之和最小．

    查看试题解析

三、解答题

  • 16. 在体育课掷实心球活动中，小华通过研究发现：实心球所经过的路线是一条抛物线的一部分，如果球出手处点 A 距离地面的高度为 2m ，当球运行的水平距离为 6m 时，达到最大高度 5m 的 B 处（如图），问实心球的落地点 C 与出手处点 A 的水平距离是多少？（结果保留根号）

    查看试题解析

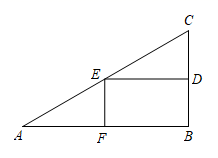
  • 17. 现有一块直角三角形的材料， AB=80 cm， BC=60 cm，用它截下一个矩形，如图是截法示意图，求这种截法下矩形的最大面积是多少？

    查看试题解析

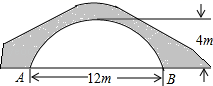
  • 18. 如图的一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线解析式是 t=−2x+80 ，求选取点B为坐标原点时的抛物线解析式．

    查看试题解析

  • 19. 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）。设每件商品的售价上涨x元（x 为正整数），每个月的销售利润为W 元．求每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    查看试题解析

  • 20. 某百货商店服装在销售过程中发现，某品牌童装平均每天可售出20件，每件盈利40元，经市场调查发现，在进货不变的情况下，若每件童装每降价1元，日销售量将增加2件，当每件童装降价多少元时，这种童装一天的销售利润最多？最多利润是多少？

    查看试题解析

  • 21. 在“学习一项体育技能”活动中，小明作为学生代表去观看“青岛黄海足球队”的训练．他看到队员们在做掷界外球训练，甲球员要将足球掷给离他7.5米远的乙球员，掷出足球的运行轨还是一条抛物线，足球行进的高度y（米）与水平距离x（米）之间的关系如图所示，足球出手时离地面的高度为2米，在距离甲球员4米处达到最大高度3.6米．若不计其他因素，身高1.85米的乙球员要能触到足球，他垂直起跳的高度至少要达到多少米？

    查看试题解析

  • 22. 某企业设计了一款工艺品，每件的成本是 50 元，为了合理定价，投放市场进行试销.据市场调查，销售单价是 100 元时，每天的销售量是 50 件，而销售单价每降低 1 元，每天就可多售出 5 件，但要求销售单价不得低于成本.求销售单价为多少元时，每天的销售利润最大？最大利润是多少？

    查看试题解析