2021-2022学年度第一学期九年级数学第22章《二次函数》22.1二次函数的图像和性质 期末复习练习卷(人教版)
试卷更新日期:2021-12-29 类型:复习试卷
一、单选题
-
1. 若函数 是二次函数,则m的值为( )A、3 B、-3 C、 D、92. 下列函数中,属于二次函数的是( )A、 B、 C、 D、3. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、
 B、
B、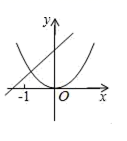 C、
C、 D、
D、 4. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、5. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线6. 二次函数 的图象的开口方向,对称轴和顶点坐标为( )A、开口向上,对称轴为直线 ,顶点 B、开口向上,对称轴为直线 ,顶点(1,5) C、开口向下,对称轴为直线 ,顶点(1, ) D、开口向上,对称轴为直线 ,顶点(1, )7. 若二次函数 的图象如图所示,则坐标原点可能是( )
4. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、5. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线6. 二次函数 的图象的开口方向,对称轴和顶点坐标为( )A、开口向上,对称轴为直线 ,顶点 B、开口向上,对称轴为直线 ,顶点(1,5) C、开口向下,对称轴为直线 ,顶点(1, ) D、开口向上,对称轴为直线 ,顶点(1, )7. 若二次函数 的图象如图所示,则坐标原点可能是( ) A、P点 B、Q点 C、M点 D、N点8. 抛物线y=(x+1)2+2上两点(0,a)、(﹣1,b),则a、b的大小关系是( )A、a>b B、b>a C、a=b D、无法比较大小9. 已知抛物线 上部分点的横坐标x 与纵坐标y的对应值如表:
A、P点 B、Q点 C、M点 D、N点8. 抛物线y=(x+1)2+2上两点(0,a)、(﹣1,b),则a、b的大小关系是( )A、a>b B、b>a C、a=b D、无法比较大小9. 已知抛物线 上部分点的横坐标x 与纵坐标y的对应值如表:…
1
2
3
4
5
…
…
-5
…
根据如表,下列判断正确的是 ( )
A、该抛物线开口向上 B、该抛物线的对称轴是直线x=1 C、该抛物线一定经过点 D、该抛物线在对称轴左侧部分y随x的增大而减小10. 抛物线 的对称轴是( )A、x= B、x=3 C、x=-3 D、x=6二、填空题
-
11. 若二次函数y=x2+bx-5的对称轴为直线x=2,则关于x的方程x2+bx-5=2x-13的解为12. 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于C点,M点在抛物线的对称轴上,当点M到点B的距离与到点C的距离之和最小时,点M的坐标为
 13. 如图,二次函数y=(x﹣1)2﹣1的图象(0≤x≤3),y的取值范围是.
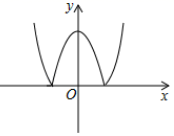
13. 如图,二次函数y=(x﹣1)2﹣1的图象(0≤x≤3),y的取值范围是. 14. 已知函数y=|x2﹣4|的大致图象如图所示,那么:方程|x2﹣4|=m . (m为实数)
14. 已知函数y=|x2﹣4|的大致图象如图所示,那么:方程|x2﹣4|=m . (m为实数)①若该方程恰有3个不相等的实数根,则m的值是 .
②若该方程恰有2个不相等的实数根,则m的取值范围是 .
 15. 已知函数 是二次函数,则m=.
15. 已知函数 是二次函数,则m=.三、解答题
-
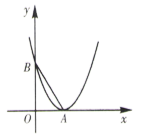
16. 当m为何值时,函数 是二次函数.17. 已知二次函数 的图象如图所示,求 的面积.
 18. 画出函数
18. 画出函数 的图象,写出它的开口方向,对称轴和顶点,并说明当y随x的增大而增大时,x的取值范围. 19. 近期,海峡两岸关系的气氛大为改善.大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售.某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
的图象,写出它的开口方向,对称轴和顶点,并说明当y随x的增大而增大时,x的取值范围. 19. 近期,海峡两岸关系的气氛大为改善.大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售.某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:每千克售价(元) 40 39 38 37 … 30 每天销量(千克) 60 65 70 75 … 110 设当单价从40元/千克下调了x元时,销售量为y千克;
(1)写出y与x间的函数关系式;
(2)如果凤梨的进价是20元/千克,若不考虑其他情况,那么单价从40元/千克下调多少元时,当天的销售利润W最大?利润最大是多少?20. 已知二次函数y=2x2﹣x+1,当﹣1≤x≤1时,求函数y的最小值和最大值.彤彤的解答如下:解:当x=﹣1时,则y=2×(﹣1)2﹣(﹣1)+1=4;
当x=1时,则y=2×12﹣1+1=2;
所以函数y的最小值为2,最大值为4.
彤彤的解答正确吗?如果不正确,写出正确的解答.