初中数学浙教版七年级上册期末复习卷第六章图形的初步知识
试卷更新日期:2021-12-28 类型:复习试卷
一、单选题
-
1. 过平面内已知点A作直线,可作直线的条数为( )A、0条 B、1条 C、2条 D、无数条2. 下列图形绕虚线旋转一周,便能形成圆锥体的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、单项式 的系数是 B、若AB=BC,则点B是线段AC的中点 C、3和5是同类项 D、连接两点的线段就是两点间的距离4. 下列各图形中,有交点的是 ( )A、
3. 下列说法正确的是( )A、单项式 的系数是 B、若AB=BC,则点B是线段AC的中点 C、3和5是同类项 D、连接两点的线段就是两点间的距离4. 下列各图形中,有交点的是 ( )A、 B、
B、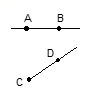 C、
C、 D、
D、 5. 如图,下列各个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )A、
5. 如图,下列各个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )A、 B、
B、 C、
C、 D、
D、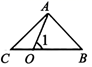 6. 如图,若∠BOC:∠AOC=1:2,∠AOB=63°,且OC在∠AOB的内部,则∠AOC=( )
6. 如图,若∠BOC:∠AOC=1:2,∠AOB=63°,且OC在∠AOB的内部,则∠AOC=( )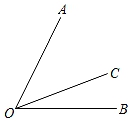 A、78° B、42° C、39° D、21°7. 如图,A、O、B在同一直线上,且 ,则 的余角有( )
A、78° B、42° C、39° D、21°7. 如图,A、O、B在同一直线上,且 ,则 的余角有( )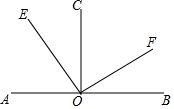 A、1个 B、2个 C、3个 D、4个8. 图中共有线段( )
A、1个 B、2个 C、3个 D、4个8. 图中共有线段( ) A、4条 B、6条 C、8条 D、10条9. 如图,线段AB=22cm,C是AB上一点,且AC=14cm,O是AB的中点,线段OC的长度是( )
A、4条 B、6条 C、8条 D、10条9. 如图,线段AB=22cm,C是AB上一点,且AC=14cm,O是AB的中点,线段OC的长度是( ) A、2cm B、3cm C、4cm D、5cm10. 已知 , , ,下面结论正确的是( )A、 B、 C、 D、
A、2cm B、3cm C、4cm D、5cm10. 已知 , , ,下面结论正确的是( )A、 B、 C、 D、二、填空题
-
11. 电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,这说明(请填入符合题意答案的序号).
①点动成线;②线动成面;③面动成体.
12. 如图,口渴的马儿在 点处想尽快地到达小河边喝水,它应该沿着线路 奔跑,依据是 . 13. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm.
13. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm. 14. ∠1和∠2互余,∠2和∠3互补,∠1=63°,∠3= .15. 把16.42° 用度分秒表示为 ;把71°4′30″用度表示为度.16. 要在墙上钉稳一根横木条,至少要钉个钉子,这样做的道理是 .17. 往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有种不同的票价,需准备种车票.18. 已知 三点在同一条直线上,线段 ,则 .19. 平面上有6个点,其中任意3个点都不在同一条直线上,若经过每两点画一条直线,则一共可以画出的直线条数是.20. 在 中,C,D分别为边 , 上的点(不与顶点O重合).对于任意锐角 ,下面三个结论:
14. ∠1和∠2互余,∠2和∠3互补,∠1=63°,∠3= .15. 把16.42° 用度分秒表示为 ;把71°4′30″用度表示为度.16. 要在墙上钉稳一根横木条,至少要钉个钉子,这样做的道理是 .17. 往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有种不同的票价,需准备种车票.18. 已知 三点在同一条直线上,线段 ,则 .19. 平面上有6个点,其中任意3个点都不在同一条直线上,若经过每两点画一条直线,则一共可以画出的直线条数是.20. 在 中,C,D分别为边 , 上的点(不与顶点O重合).对于任意锐角 ,下面三个结论:①点C和点D有无数个;
②连接 ,存在 是直角;
③点C到边 的距离不超过线段 的长.
所有正确结论的序号是.
三、计算题
-
21. 计算 .
四、解答题
-
22. 若一个角的余角是这个角的 ,求这个角的补角.23. 如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=120°,求∠COD的度数.
 24. 如图,已知点C、D在线段AB上,点D是AB中点,AC= AB,CD=2.求线段AB长.
24. 如图,已知点C、D在线段AB上,点D是AB中点,AC= AB,CD=2.求线段AB长.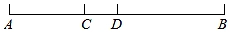 25. 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=40°,求∠BOF的度数.
25. 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=40°,求∠BOF的度数.
五、综合题
-
26. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
 (1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°
(1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请直接写出所有满足题意t的取值 ,若不存在,请说明理由;
②在旋转的过程中,当边AB与射线OE相交时,如图3,请直接写出∠AOC﹣∠BOE的值 .
-