湖南省株洲市醴陵市2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 将一元二次方程3x²=﹣2x+5化为一般形式后，二次项系数、一次项系数、常数项分别为（）

A、3、﹣2、5 B、3、2、﹣5 C、3、﹣2、﹣5 D、3、5、﹣2

查看试题解析
2. $2 \cos 60 °$ 的值等于（）．

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
3. 用配方法解一元二次方程x²﹣4x﹣1=0，配方后得到的方程是（　　）

A、（x﹣2）²=1 B、（x﹣2）²=4 C、（x﹣2）²=5 D、（x﹣2）²=3

查看试题解析
4. 已知点A（x₁ ， y₁），B（x₂ ， y₂）是反比例函数y＝ $\frac{3}{x}$ 的图象上的两点，若x₁＜0＜x₂ ，则下列结论正确的是（）

A、y₁＜0＜y₂ B、y₂＜0＜y₁ C、y₁＜y₂＜0 D、y₂＜y₁＜0

查看试题解析
5. 生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下 $a$ 与全身 $b$ 的高度比值接近0.618，可以增加视觉美感，若图中 $b$ 为2米，则 $a$ 约为（）

A、1.24米 B、1.38米 C、1.42米 D、1.62米

查看试题解析
6. 如图，点E是 $▱ A B C D$ 的边 $A D$ 上的一点，且 $\frac{D E}{A E} = \frac{1}{2}$ ，连接 $B E$ 并延长交 $C D$ 的延长线于点F，若 $D E = 3 ， D F = 4$ ，则 $▱ A B C D$ 的周长为（）

A、21 B、28 C、34 D、42

查看试题解析
7. 如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60海里的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离是（）

A、30海里 B、60海里 C、120海里 D、（30＋30 $\sqrt{3}$ ）海里

查看试题解析
8. 关于抛物线 $y = {(x - 1)}^{2} - 2$ ，下列说法错误的是（）

A、开口方向向上 B、对称轴是直线 $x = 1$ C、顶点坐标为 $(- 1 ， - 2)$ D、当 $x > 1$ 时， $y$ 随 $x$ 的增大而增大

查看试题解析
9. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”，“兵”所在位置的格点构成的三角形相似（）

A、①处 B、②处 C、③处 D、④处

查看试题解析
10. 如图，已知正方形ABCD，E为AB的中点，F是AD边上的一个动点，连接EF，将△AEF沿EF折叠得△HEF，延长FH交BC于M，现在有如下5个结论：①△BEM≌△HEM；②△EFM一定是直角三角形；③当M与C重合时，有DF＝2AF；④MF平分正方形ABCD的面积；⑤ $F H \cdot M H = \frac{1}{4} A B^{2}$ ；在以上5个结论中，正确的有（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 点（2，3）双曲线 $y = \frac{6}{x}$ 的图象上.（填“在”或“不在”）

查看试题解析
12. 已知 $\frac{a}{b} = \frac{3}{5}$ ，则代数式 $\frac{2 a + b}{2 a - b}$ 的值是.

查看试题解析
13. 关于x的一元二次方程 $x^{2} - 2 x - m = 0$ 有两个不相等的实数根，则m的最小整数值是．

查看试题解析
14. 如图：在Rt△ABC，∠C＝90°，点D是AC边上的一点，DE垂直平分AB，垂足为E，若AC＝4，BC＝3，则线段DE的长度为.

查看试题解析
15. 某市对九年级学生进行“综合素质”评价，评价结果分为 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 五个等级.现随机抽取了5000名学生的评价结果作为样本进行分析，绘制了如图所示的统计图.已知图中从左到右的五个长方形的高之比为 $2 ： 3 ： 3 ： 1 ： 1$ ，据此估算该市10000名九年级学生中“综合素质”评价结果为“ $A$ ”的学生约为人.

查看试题解析
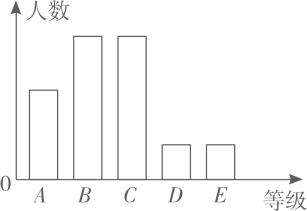16. 已知二次函数y＝4x²﹣mx+5，当x≤﹣2时，y随x的增大而减小；当x≥﹣2时，y随x的增大而增大，则当x＝1时，y的值为.

查看试题解析
17. 设a、b是方程x²+x﹣2020=0的两个实数根，则（a﹣1）（b﹣1）的值为.

查看试题解析
18. 如图，在平面直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $(- 4 ， 0)$ 、 $(0 ， 4)$ ，点 $C (3 ， n)$ 在第一象限内，连接 $A C$ 、 $B C$ .已知 $∠ B C A = 2 ∠ C A O$ ，则 $n =$ .

查看试题解析

三、解答题

19.

(1)、计算：（﹣2）²＋2sin60°﹣tan60°；

(2)、解方程：x²﹣2x＝1

查看试题解析
20. 对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境.为了调查同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取部分同学进行问卷测试，把测试成绩分成“优、良、中、差”四个等级，绘制了不完整的统计图：
根据以上统计信息，解答下列问题：

(1)、求成绩是“优”的人数占抽取人数的百分比；

(2)、求本次随机抽取问卷测试的人数；

(3)、请把条形统计图补充完整；

(4)、若该校学生人数为4000人，请估计成绩是“优”和“良”的学生共有多少人？

查看试题解析
21. 某商场将进货价为30元的台灯以40元售出，平均每月能售出600个，调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个．为了实现平均每月10000元的销售利润，商场决定采取调控价格的措施，扩大销售量，减少库存，这种台灯的售价应定为多少元?这时应进台灯多少个?

查看试题解析
22. 某校为检测师生体温，在校门安装了某型号测温门.如图为该测温门截面示意图，已知测温门AD的顶部A处距地面高为2.2m，为了解自己的有效测温区间.身高1.6m的小聪做了如下实验：当他在地面N处时测温门开始显示额头温度，此时在额头B处测得A的仰角为30°；在地面M处时，测温门停止显示额头温度，此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.（额头到地面的距离以身高计，计算精确到0.1m， $\sqrt{3}$ ≈1.73， $\sqrt{2}$ ≈1.41）

查看试题解析
23. 如图，在正方形ABCD中，E是边AD上的点，点F在边CD上，且CF＝3FD，∠BEF＝90°

(1)、求证：△ABE∽△DEF；

(2)、若AB＝6，延长EF交BC的延长线于点G，求BG的长.

查看试题解析
24. 已知平行四边形ABCD的两邻边AB，AD的长是关于x的方程x²﹣mx＋2＝0的两个实数根.

(1)、若AB＝2，那么平行四边形ABCD的周长是多少？

(2)、当m为何值时，平行四边形ABCD是菱形？求出这时菱形的边长.

查看试题解析
25. 如图，直线 $y_{1} = a x + 1$ 经过点A（﹣2，0），且与x轴、y轴分别相交于A、B两点，与双曲线 $y_{2} = \frac{k}{x}$ （x $>$ 0）相交于点P，PC⊥x轴于点C，且PC＝2.

(1)、求这条直线及双曲线的解析式；

(2)、若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与 $△ A O B$ 相似时，求点Q的坐标.（点Q的纵坐标，可以不化成最简形式）

查看试题解析
26. 如图，在平面直角坐标系中，已知点B的坐标为（﹣2，0），且OA＝OC＝4OB，抛物线y＝ax²＋bx＋c（a≠0）图象经过A，B，C三点.

(1)、求A，C两点的坐标；

(2)、求抛物线的解析式；

(3)、若点P是直线AC下方的抛物线上的一个动点，作PD⊥AC于点D，当PD的值最大时，求此时点P的坐标及PD的最大值.

查看试题解析