湖南省株洲市荷塘区2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 对于函数 , 下列说法错误的是( )A、当时,的值随的增大而增大 B、当时,的值随的增大而减小 C、它的图象分布在第一、三象限 D、它的图象既是轴对称图形又是中心对称图形2. a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣ 的图象上,则( )A、a<b<0 B、b<a<0 C、a<0<b D、b<0<a3. 将二次函数y=(x+1)2-2的图象沿x轴向右平移2个单位长度,所得抛物线对应的函数表达式为( )A、y=(x+3)2-2 B、y=(x+3)2+2 C、y=(x-1)2+2 D、y=(x-1)2-24. 一元二次方程x2+4x﹣3=0的两根为x1、x2 , 则x1•x2的值是( )A、4 B、﹣4 C、3 D、﹣35. 王叔叔从市场上买了一块长80 cm,宽70 cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长为x cm的正方形后,剩余的部分刚好能围成一个底面积为3000 cm2的无盖长方体工具箱.根据题意可列方程为 ( )
 A、(80-x)(70-x)=3000 B、80×70-4x2=3000 C、(80-2x)(70-2x)=3000 D、80×70-4x2-(70+80)x=30006. 如图,从点C观测点D的仰角是( )
A、(80-x)(70-x)=3000 B、80×70-4x2=3000 C、(80-2x)(70-2x)=3000 D、80×70-4x2-(70+80)x=30006. 如图,从点C观测点D的仰角是( )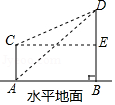 A、∠DAB B、∠DCE C、∠DCA D、∠ADC7. 在平面直角坐标系中,点 , 的坐标分别是 , , 以点为位似中心,相似比为 , 把缩小,得到 , 则点的对应点的坐标为( )A、或 B、或 C、或 D、或8. 已知 , , 则=( )A、2 B、 C、3 D、9. 如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )
A、∠DAB B、∠DCE C、∠DCA D、∠ADC7. 在平面直角坐标系中,点 , 的坐标分别是 , , 以点为位似中心,相似比为 , 把缩小,得到 , 则点的对应点的坐标为( )A、或 B、或 C、或 D、或8. 已知 , , 则=( )A、2 B、 C、3 D、9. 如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )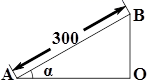 A、米 B、米 C、米 D、米10. 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
A、米 B、米 C、米 D、米10. 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( ) A、①② B、①④ C、②③ D、②④
A、①② B、①④ C、②③ D、②④二、填空题
-
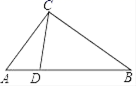
11. 已知函数 是反比例函数,则m的值为 .12. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为
 13. 若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是.14. 抛物线的顶点坐标是.15. 为从甲、乙、丙三名射击运动员中选一人参加全运会,教练把他们的10次比赛成绩做了统计:平均成绩均为9.3环,方差分别是 , , , 应该选参加全运会.16. 如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)
13. 若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是.14. 抛物线的顶点坐标是.15. 为从甲、乙、丙三名射击运动员中选一人参加全运会,教练把他们的10次比赛成绩做了统计:平均成绩均为9.3环,方差分别是 , , , 应该选参加全运会.16. 如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母) 17. a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是bc(用“>”或“<”号填空)18. 对于3个数: , 用表示这三个数的中位数,用表示这三个数的最大数.例如:.如果 , 则=.
17. a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是bc(用“>”或“<”号填空)18. 对于3个数: , 用表示这三个数的中位数,用表示这三个数的最大数.例如:.如果 , 则=.三、解答题
-
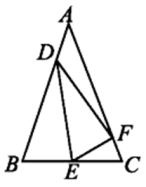
19. 计算: .20. 如图,在中, , 点在边上,满足 , 且点 , 分别在边 , 上. 求证:.
 21. 在对某地区一次人口抽样统计中,各年龄段的人数如表所示(年龄为整数).请根据此表回答下列问题:
21. 在对某地区一次人口抽样统计中,各年龄段的人数如表所示(年龄为整数).请根据此表回答下列问题:年龄
0~9
10~19
20~29
30~39
40~49
50~59
60~69
70~79
80~89
人数
9
11
17
18
17
12
8
6
2
(1)、这次抽样的样本容量是;(2)、在这个样本中,年龄的中位数位于哪个年龄段内;(3)、在这个样本中,年龄在60岁以上(含60岁)的频率是;(4)、如果该地区有人口80 000,为关注人口老龄化问题,请估算该地区60岁以上(含60岁)的人口数.22. 如图,某船由西向东航行,在点A测得小岛O在北偏东60°,船航行了10海里后到达点B,这时测得小岛O在北偏东45°,船继续航行到点C时,测得小岛O恰好在船的正北方,求此时船到小岛的距离.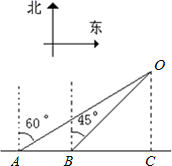 23. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于点 , 且过点.
23. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于点 , 且过点.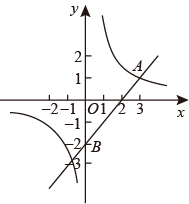 (1)、求反比例函数和一次函数的表达式;(2)、如果点是轴上一点,且的面积是3,求点的坐标.24. 已知关于 的一元二次方程 有两个不相等的实数根 .(1)、求 的取值范围;(2)、若 ,求 的值及方程的根.25. 攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量y(千克)与该天的售价x(元/千克)之间的数量满足如下表所示的一次函数关系.
(1)、求反比例函数和一次函数的表达式;(2)、如果点是轴上一点,且的面积是3,求点的坐标.24. 已知关于 的一元二次方程 有两个不相等的实数根 .(1)、求 的取值范围;(2)、若 ,求 的值及方程的根.25. 攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量y(千克)与该天的售价x(元/千克)之间的数量满足如下表所示的一次函数关系.销售量y(千克)
…
32.5
35
35.5
38
…
售价x(元/千克)
…
27.5
25
24.5
22
…
(1)、某天这种芒果售价为28元/千克.求当天该芒果的销售量(2)、设某天销售这种芒果获利m元,写出m与售价x之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?26. 如图,抛物线与轴交于 , 两点,抛物线上另有一点在轴下方,且使△OCA△OBC.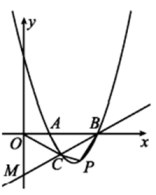 (1)、求线段的长度;(2)、设直线与轴交于点 , 当平分的面积时,求抛物线的解析式;(3)、在(2)的条件下,直线下方抛物线上是否存在一点 , 使得四边形的面积最大?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求线段的长度;(2)、设直线与轴交于点 , 当平分的面积时,求抛物线的解析式;(3)、在(2)的条件下,直线下方抛物线上是否存在一点 , 使得四边形的面积最大?若存在,请求出点的坐标;若不存在,请说明理由.