湖南省长沙市长沙县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 方程化为一般形式后二次项系数、一次项系数和常数项分别为( )A、1,1,-2 B、1,-3,6 C、1,-3,2 D、1,3,22. 下列关系式中,y是x反比例函数的是( )A、y= x B、y=- C、y=3x2 D、y=6x+13. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 解方程 , 可用配方法将其变形为( )A、 B、 C、 D、5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 如图,在中,∠ABC=50°,则∠AOC等于( )
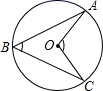 A、50° B、80° C、100° D、130°7. 已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )A、2:3 B、4:9 C、16:81 D、9:48. 圆心角为90°,半径为10的扇形的面积为( )A、25π B、20π C、12.5π D、5π9. 国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )A、 B、 C、 D、10. 如图,点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A、50° B、80° C、100° D、130°7. 已知两个相似三角形的相似比为4:9,则这两个三角形的对应高的比为( )A、2:3 B、4:9 C、16:81 D、9:48. 圆心角为90°,半径为10的扇形的面积为( )A、25π B、20π C、12.5π D、5π9. 国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )A、 B、 C、 D、10. 如图,点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )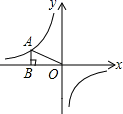 A、2 B、4 C、8 D、1611. 关于x的一元二次方程x2+px+q=0的两根同为负数,则( )A、p>0且q>0 B、p>0且q<0 C、p<0且q>0 D、p<0且q<012. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、
A、2 B、4 C、8 D、1611. 关于x的一元二次方程x2+px+q=0的两根同为负数,则( )A、p>0且q>0 B、p>0且q<0 C、p<0且q>0 D、p<0且q<012. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、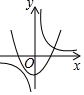 B、
B、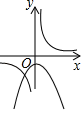 C、
C、 D、
D、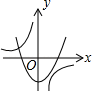
二、填空题
-
13. 取一个数作为反比例函数中k的值,使得该函数图象在第二、四象限.14. 圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于.15. 把抛物线y= x2向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是16. 如图,已知AB,CD是☉O的直径, 弧AE= 弧AC ,∠AOE=32°,那么∠COE的度数为度.
 17. 如图是用杠杆撬石头的示意图,是支点,当用力压杠杆的端时,杠杆绕点转动,另一端向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的端必须向上翘起 , 已知杠杆的动力臂与阻力臂之比为6:1,要使这块石头滚动,至少要将杠杆的端向下压.
17. 如图是用杠杆撬石头的示意图,是支点,当用力压杠杆的端时,杠杆绕点转动,另一端向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的端必须向上翘起 , 已知杠杆的动力臂与阻力臂之比为6:1,要使这块石头滚动,至少要将杠杆的端向下压.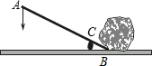 18. 如图,六边形ABCDEF为的内接正六边形,点M为劣弧上的一个动点,连接OM,以点O为旋转中心,将线段OM逆时针旋转60°得到线段ON,连接MN,得到△OMN,点H为△MON的外心.
18. 如图,六边形ABCDEF为的内接正六边形,点M为劣弧上的一个动点,连接OM,以点O为旋转中心,将线段OM逆时针旋转60°得到线段ON,连接MN,得到△OMN,点H为△MON的外心. (1)、连接MH,NH,则∠MHN=.(2)、若正六边形ABCDEF的周长为 , 当点M从点A运动到点C时,外心H所经过的路径长为.
(1)、连接MH,NH,则∠MHN=.(2)、若正六边形ABCDEF的周长为 , 当点M从点A运动到点C时,外心H所经过的路径长为.三、解答题
-
19. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
 (1)、点A的坐标为 , 点B的坐标为 , 点C的坐标为.(2)、以原点O为位似中心,将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1,请在网格内画出△A1B1C1.20. 已知反比例函数y=(m为常数)的图象在第一、三象限
(1)、点A的坐标为 , 点B的坐标为 , 点C的坐标为.(2)、以原点O为位似中心,将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1,请在网格内画出△A1B1C1.20. 已知反比例函数y=(m为常数)的图象在第一、三象限 (1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0).求出函数解析式.21. 已知关于x的方程有实数根.(1)、求m的取值范围;(2)、若2是原方程的一个根,求m的值.22. 某商场计划购进一批书包,市场调查发现:当某种进货价格为30元的书包以40元的价格出售时,平均每月售出600个,并且书包的售价每提高1元,每月销售量就减少10个.(1)、当售价定为42元时,每月可售出个;(2)、若书包的月销售量为300个,则每个书包的定价为元;(3)、当商场每月获得10000元的销售利润时,为体现“薄利多销”的销售原则,你认为销售价格应定为多少元?23. 如图,在平行四边形ABCD中,E为BC边上一点,连接AE,DE,已知∠AED=∠B.
(1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0).求出函数解析式.21. 已知关于x的方程有实数根.(1)、求m的取值范围;(2)、若2是原方程的一个根,求m的值.22. 某商场计划购进一批书包,市场调查发现:当某种进货价格为30元的书包以40元的价格出售时,平均每月售出600个,并且书包的售价每提高1元,每月销售量就减少10个.(1)、当售价定为42元时,每月可售出个;(2)、若书包的月销售量为300个,则每个书包的定价为元;(3)、当商场每月获得10000元的销售利润时,为体现“薄利多销”的销售原则,你认为销售价格应定为多少元?23. 如图,在平行四边形ABCD中,E为BC边上一点,连接AE,DE,已知∠AED=∠B. (1)、求证:△ABE∽△DEA;(2)、若AE=2,求AD·BE的值.24. 如图,AB为的直径,E为上一点,点C为的中点,过点C作直线CD垂直直线AE,垂足为D.
(1)、求证:△ABE∽△DEA;(2)、若AE=2,求AD·BE的值.24. 如图,AB为的直径,E为上一点,点C为的中点,过点C作直线CD垂直直线AE,垂足为D.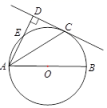 (1)、求证:DC为的切线;(2)、若AB=4,∠CAD=30°,求AC.25. 阅读材料,我们约定:若正实数a、b、c满足,其中一个数的平方等于另外两个数的乘积,则称实数a、b、c为精彩实数组.
(1)、求证:DC为的切线;(2)、若AB=4,∠CAD=30°,求AC.25. 阅读材料,我们约定:若正实数a、b、c满足,其中一个数的平方等于另外两个数的乘积,则称实数a、b、c为精彩实数组. (1)、判断实数1、2、3是否为精彩实数组,请说明理由;(2)、若a=4,b=9,且实数a、b、c为精彩实数组.求c的值;(3)、四边形ABCD,AD//BC,AD⊥CD,BC>AD,AB⊥AC,BD平分∠ABC,求证:△ABC的三边长是精彩实数组.(提示:证明AC2=AB·BC)26. 如图,抛物线与x轴交于点A( , 0),B(3,0)两点,与y轴交于点C(0,3),点D为第一象限内抛物线上的一动点,连接OD,交直线BC于点E.
(1)、判断实数1、2、3是否为精彩实数组,请说明理由;(2)、若a=4,b=9,且实数a、b、c为精彩实数组.求c的值;(3)、四边形ABCD,AD//BC,AD⊥CD,BC>AD,AB⊥AC,BD平分∠ABC,求证:△ABC的三边长是精彩实数组.(提示:证明AC2=AB·BC)26. 如图,抛物线与x轴交于点A( , 0),B(3,0)两点,与y轴交于点C(0,3),点D为第一象限内抛物线上的一动点,连接OD,交直线BC于点E. (1)、求抛物线的解析式;(2)、当△BCD的面积为△ABC面积的时,求点D的横坐标;(3)、若△CDE的面积为 , △OCE面积为 , 请判断是否有最大值,若有,请求出这个最大值;若没有,请说明理由.
(1)、求抛物线的解析式;(2)、当△BCD的面积为△ABC面积的时,求点D的横坐标;(3)、若△CDE的面积为 , △OCE面积为 , 请判断是否有最大值,若有,请求出这个最大值;若没有,请说明理由.