湖南省湘西土家族苗族自治州龙山县2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 若关于 $x$ 的一元二次方程 $x^{2} - 4 x + 2 m = 0$ 的常数项是4，则 $m$ 等于（）

A、1 B、2 C、3 D、4

查看试题解析
2. 关于 $x$ 的一元二次方程 $(a - 1) x^{2} + a x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 值为（）

A、-1 B、0 C、1 D、1

查看试题解析
3. 一元二次方程 $3 x^{2} - 5 x + 2 = 0$ 根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
4. 如图，将一个含30°角的直角三角板 $A B C$ 绕点 $A$ 顺时针旋转得到 $△ A B C$ ，点 $B$ 、 $A$ 、 $C$ 在同一条直线上，则旋转角 $∠ B A B$ 的度数是（）

A、60° B、90° C、120° D、150°

查看试题解析
5. 若点 $M (2, b - 3)$ 关于原点对称点 $N$ 的坐标是 $(- 3 - a, 2)$ ，则 $a, b$ 的值为（）

A、 $a = - 1, b = 1$ B、 $a = 1, b = - 1$ C、 $a = 1, b = 1$ D、 $a = - 1, b = - 1$

查看试题解析
6. 如图，扇形的半径为 $6 c m$ ，圆心角为120°，则该扇形的面积为（）

A、 $6 π c m^{2}$ B、 $9 π c m^{2}$ C、 $12 π c m^{2}$ D、 $18 π c m^{2}$

查看试题解析
7. 如图，⊙O中，半径OC⊥弦AB于点D，点E在⊙O上，∠E=22.5°，AB=4，则半径OB等于（）

A、 $\sqrt{2}$ B、2 C、2 $\sqrt{2}$ D、3

查看试题解析
8. 如图， $A B$ 为 $⊙ O$ 的一条固定直径，自左半圆上一点 $C$ ，作弦 $C D ⊥ A B$ ， $∠ O C D$ 的平分线交 $⊙ O$ 于点 $E$ ，当点 $C$ 在左半圆（不包括 $A$ ， $B$ 两点）上移动时，关于点 $E$ 的说法：
①到 $C D$ 的距离始终不变；②位置始终不变；③始终平分 $\overset{⌢}{D B}$ ；④位置随点 $C$ 的移动而移动.正确的是（）

A、①② B、②③ C、② D、④

查看试题解析
9. 定义符号min{a，b}的含义为：当a≥b时min{a，b}=b；当a＜b时min{a，b}=a．如：min{1，﹣3}=﹣3，min{﹣4，﹣2}=﹣4．则min{﹣x²+1，﹣x}的最大值是（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、1 D、0

查看试题解析

二、多选题

10. 对于二次函数 $y = 2 {(x - 1)}^{2}$ ，下列说法不正确的是（）

A、图象开口向下 B、图象的对称轴是直线 $x = 1$ C、函数最大值为0 D、 $y$ 随 $x$ 的增大而增大

查看试题解析

三、填空题

11. 方程 $x (x - 5) = 0$ 的解是.

查看试题解析
12. 若关于 $x$ 的一元二次方程 $k x^{2} + x - 1 = 0$ 有两个不相等的实数根，则实数 $k$ 的取值范围是.

查看试题解析
13. 我市某公司前年缴税40万元，今年缴税48.4万元．该公司缴税的年平均增长率为．

查看试题解析
14. 抛物线 $y = x^{2} - 4 x - 3$ 的顶点坐标是.

查看试题解析
15. 如图，抛物线 $y = a x^{2}$ 与直线 $y = b x + c$ 的两个交点坐标分别为 $A (- 2 ， 4)$ ， $B (1 ， 1)$ ，则关于 $x$ 的方程 $a x^{2} - b x - c = 0$ 的解为.

查看试题解析
16. 如图，所示的美丽图案中，既是轴对称图形又是中心对称图形的有个.

查看试题解析
17. 已知⊙O的半径是一元二次方程x²+6x﹣16＝0的解，且点O到直线AB的距离是 $\sqrt{2}$ ，则直线AB与⊙O的位置关系是.

查看试题解析
18. 已知二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象如图所示，对称轴是 $x = - \frac{1}{4}$ ，经过点 $(1 ， 0)$ 和点 $(0 ， 2)$ .在下列五个结论中：① $a b c < 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a - b + c > 0$ ；④当 $x > - \frac{1}{4}$ 时， $y > 0$ ；正确的个数有个.

查看试题解析

四、解答题

19. 用适当的方法解下列方程.

(1)、 $x^{2} - x - 2 = 0$ ；

(2)、 $3 {(x - 2)}^{2} = x (x - 2)$ .

查看试题解析
20. 已知关于 $x$ 的方程 $x^{2} + a x + a - 1 = 0$ .

(1)、若该方程的一个根为2，求 $a$ 的值及方程的另一个根；

(2)、求证：不论 $a$ 取何实数，该方程都有两个实数根.

查看试题解析
21. 已知二次函数 $y = x^{2} - 3 x + m$ 与 $x$ 轴没有交点.

(1)、求 $m$ 的取值范围；

(2)、当 $x$ 取何值时， $y$ 随 $x$ 的增大而减小.

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 8 c m$ ， $B C = 10 c m$ ，点 $P$ 由点 $A$ 出发，沿 $A B$ 边以 $1 c m / s$ 的速度向点 $B$ 移动，点 $Q$ 由点 $B$ 出发，沿 $B C$ 边以 $2 c m / s$ 的速度向点 $C$ 移动，如果点 $P$ 、 $Q$ 分别从点 $A$ 、 $B$ 同时出发，求：经过几秒后 $△ P B Q$ 的面积等于 $15 c m^{2}$ ？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $C B = 6$ ， $C A = 8$ ，将 $△ A B C$ 绕点 $B$ 顺时针旋转得到 $△ D B E$ ，使点 $C$ 的对应点 $E$ 恰好落在 $A B$ 上，求线段 $A E$ 的长.

查看试题解析
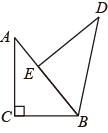24. 已知：如图AB为⊙O直径，C是⊙O上一点，D在AB的延长线上，∠DCB＝∠A．

(1)、求证：CD是⊙O的切线．

(2)、若CD与⊙O相切，且∠D＝30°，BD＝10，求⊙O的半径．

查看试题解析
25. 阅读理解：
材料一：若一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ）的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ .
材料二：已知实数 $m$ ， $n$ 满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，求 $\frac{n}{m} + \frac{m}{n}$ 的值.
解：由题知 $m$ ， $n$ 是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根，根据材料一得 $m + n = 1$ ， $m n = - 1$ ，
∴ $\frac{n}{m} + \frac{m}{n} = \frac{m^{2} + n^{2}}{m n} = \frac{{(m + n)}^{2} - 2 m n}{m n} = \frac{1 + 2}{- 1} = - 3$ .
解决问题：

(1)、已知实数 $s$ ， $t$ 满足 $2 s^{2} - 2 s - 1 = 0$ ， $2 t^{2} - 2 t - 1 = 0$ ，且 $s \neq t$ ，求 $s^{2} t + s t^{2}$ 的值；

(2)、已知实数 $p$ ， $q$ 满足 $p^{2} = 3 p + 2$ ， $2 q^{2} = 3 q + 1$ ，且 $p \neq 2 q$ ，求 $p^{2} + 4 q^{2}$ 的值.

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，直线 $l$ ： $y = \frac{3}{4} x + m$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 和点 $B (0 ， - 1)$ ，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点 $B$ ，且与直线 $l$ 的另一个交点为 $C (4 ， n)$ .

(1)、求 $n$ 的值和抛物线的解析式；

(2)、 $M$ 是平面内一点，将 $△ A O B$ 绕点 $M$ 沿逆时针方向旋转90°后，得到 $△ A_{1} O_{1} B_{1}$ ，点 $A$ 、 $O$ 、 $B$ 的对应点分别是点 $A_{1}$ 、 $O_{1}$ 、 $B_{1}$ ，若 $△ A_{1} O_{1} B_{1}$ 的两个顶点恰好落在抛物线上，请直接写出点 $A_{1}$ 的横坐标.

查看试题解析