湖南省邵阳市新邵县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 已知点在反比例函数的图象上,则该函数表达式为( )A、 B、 C、 D、2. 如图,小红同学测量一棵与地面垂直的树的高度时,在距离树的底端米的处,测得树顶的仰角 , 借助计算器计算树的高度,下列按键顺序正确的是( )
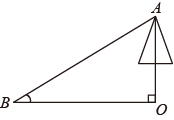 A、 B、 C、 D、3. 用求根公式法解方程的解是( )A、 B、 C、 D、4. 如图,在平行四边形中,点在边上, ,连接交于点 , 则的面积与的面积之比为( )
A、 B、 C、 D、3. 用求根公式法解方程的解是( )A、 B、 C、 D、4. 如图,在平行四边形中,点在边上, ,连接交于点 , 则的面积与的面积之比为( )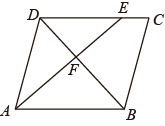 A、 B、 C、 D、5. 对于二次函数 的图象,下列说法正确的是( )A、开口向下; B、对称轴是直线x=-1; C、顶点坐标是(-1,2); D、与x轴没有交点.6. 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为( )
A、 B、 C、 D、5. 对于二次函数 的图象,下列说法正确的是( )A、开口向下; B、对称轴是直线x=-1; C、顶点坐标是(-1,2); D、与x轴没有交点.6. 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为( )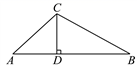 A、2 B、2 C、+1 D、+17. 从总体中抽取一部分数据作为样本去估计总体的某种属性,下面叙述正确的是( )A、样本容量越大,样本平均数越大 B、样本容量越大,样本方差就越小 C、样本容量越小,样本平均数和方差越大 D、样本容量越大,对总体的估计就越准确8. 如图,以点为位似中心,把放大为原图形的2倍得到 , 若与的位似比为 , 则以下结论中正确的是( )
A、2 B、2 C、+1 D、+17. 从总体中抽取一部分数据作为样本去估计总体的某种属性,下面叙述正确的是( )A、样本容量越大,样本平均数越大 B、样本容量越大,样本方差就越小 C、样本容量越小,样本平均数和方差越大 D、样本容量越大,对总体的估计就越准确8. 如图,以点为位似中心,把放大为原图形的2倍得到 , 若与的位似比为 , 则以下结论中正确的是( )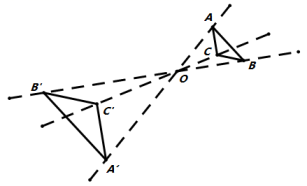 A、 B、 C、 D、9. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
A、 B、 C、 D、9. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( ) A、2cm B、5cm C、6cm D、7cm10. (古代数学问题)直田积八百六十四步,只云长阔共六十步,问长多阔几何.——摘自古代数学家杨辉的《田亩比类乘除捷法》译文:一块矩形田地的面积为平方步,只知道它的长与宽共步,则它的长比宽多( )A、6 B、12 C、24 D、36
A、2cm B、5cm C、6cm D、7cm10. (古代数学问题)直田积八百六十四步,只云长阔共六十步,问长多阔几何.——摘自古代数学家杨辉的《田亩比类乘除捷法》译文:一块矩形田地的面积为平方步,只知道它的长与宽共步,则它的长比宽多( )A、6 B、12 C、24 D、36二、填空题
-
11. 一元二次方程有一根为 , 则另一个根为.12. 如图,点在的边上,要判断 , 还请你添加一个条件:.
 13. 已知 , 则.14. 已知直线与反比例函数的图象的一个交点坐标为 , 则它们的另一个交点坐标为.15. 已知是的三个内角,若 , 且均为锐角,则的度数为.16. 某校中学生开展社会实践活动,同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量,整理后制作了如图所示的统计图,请你根据统计图估计该小区每户一周内使用环保方便袋 个.
13. 已知 , 则.14. 已知直线与反比例函数的图象的一个交点坐标为 , 则它们的另一个交点坐标为.15. 已知是的三个内角,若 , 且均为锐角,则的度数为.16. 某校中学生开展社会实践活动,同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量,整理后制作了如图所示的统计图,请你根据统计图估计该小区每户一周内使用环保方便袋 个. 17. 如图,对于一条给定的线段 , 找出它的黄金分割点的作法如下:
17. 如图,对于一条给定的线段 , 找出它的黄金分割点的作法如下:
(1)过点作 , 并在垂线上取;
(2)连接 , 以点为圆心,长为半径画弧交于点;
(3)以点为圆心,长为半径画弧交于点.
则点为线段的黄金分割点,的长为.
 18. 如图,抛物线与直线的两个交点坐标分别为 , 则关于的不等式的解集为.
18. 如图,抛物线与直线的两个交点坐标分别为 , 则关于的不等式的解集为.
三、解答题
-
19. 计算:20. 已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+1=0有两个实数根x1 , x2 ,(1)、求k的取值范围.(2)、若x1x2与x1+x2互为相反数,试求k的值.21. 如图,在平面直角坐标系中,反比例函数的图象经过点 , 过点作轴,垂足为点且的面积为.
 (1)、求与的值;(2)、若点也在反比例函数的图象上,求当时,函数值的取值范围.22. 某校开展了“阅读战‘疫'读书强国”为主题的阅读活动,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理后,绘制出以下两幅不完整的统计图,请根据图①和图②提供的信息,解答下列问题:
(1)、求与的值;(2)、若点也在反比例函数的图象上,求当时,函数值的取值范围.22. 某校开展了“阅读战‘疫'读书强国”为主题的阅读活动,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理后,绘制出以下两幅不完整的统计图,请根据图①和图②提供的信息,解答下列问题: (1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图①)补充完整,并计算扇形统计图中体育类所对应圆心角的度数.(3)、请你估计该校5000名学生中大约有多少人喜爱体育和艺术类书籍?
(1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图①)补充完整,并计算扇形统计图中体育类所对应圆心角的度数.(3)、请你估计该校5000名学生中大约有多少人喜爱体育和艺术类书籍? 23. 如图,在四边形中,平分 , 点为的中点.
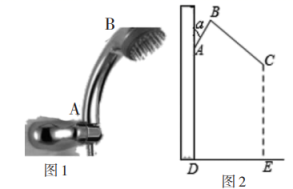
23. 如图,在四边形中,平分 , 点为的中点. (1)、求证:(2)、若 , 求的值.24. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长与墙壁的夹角 ,喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使.问:安装师傅应将支架固定在离地面多高的位置?
(1)、求证:(2)、若 , 求的值.24. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长与墙壁的夹角 ,喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使.问:安装师傅应将支架固定在离地面多高的位置?(结果精确到 , 参考数据:)
 25. 2020年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式.某乡镇贸易公司因此开设了一家网店,销售当地某种农产品.已知该农产品成本为每千克10元.调查发现,每天销售量与销售单价(元)满足如图所示的函数关系(其中).
25. 2020年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式.某乡镇贸易公司因此开设了一家网店,销售当地某种农产品.已知该农产品成本为每千克10元.调查发现,每天销售量与销售单价(元)满足如图所示的函数关系(其中).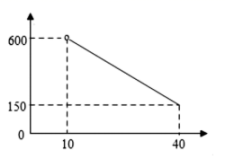 (1)、写出与之间的函数关系式.(2)、当销售单价为多少元时,每天的销售利润可达到6000元?26. 如图,二次函数的图象与轴交于两点,与轴相交于点.连接两点的坐标分别为 , 且它的图象关于直线对称
(1)、写出与之间的函数关系式.(2)、当销售单价为多少元时,每天的销售利润可达到6000元?26. 如图,二次函数的图象与轴交于两点,与轴相交于点.连接两点的坐标分别为 , 且它的图象关于直线对称 (1)、求抛物线的函数关系式;(2)、若点同时从点出发,均以每秒2个单位长度的速度分别沿边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为秒时,连接 , 将沿翻折,点恰好落在边上的处,求的值及点的坐标;(3)、在(2)的条件下,二次函数图象的对称轴上是否存在点 , 使得以为顶点的三角形与相似?如果存在,请求出点的坐标;如果不存在,请说明理由.
(1)、求抛物线的函数关系式;(2)、若点同时从点出发,均以每秒2个单位长度的速度分别沿边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为秒时,连接 , 将沿翻折,点恰好落在边上的处,求的值及点的坐标;(3)、在(2)的条件下,二次函数图象的对称轴上是否存在点 , 使得以为顶点的三角形与相似?如果存在,请求出点的坐标;如果不存在,请说明理由.