湖南省邵阳市绥宁县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 若、是方程的两个解,则代数式的值为( )A、8 B、10 C、12 D、142. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
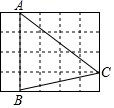 A、 B、 C、 D、3. 如图,在平面直角坐标系中,反比例函数 的图象上有A、B两点,它们的横坐标分别为2和4, 的面积为6,则 的值为( )
A、 B、 C、 D、3. 如图,在平面直角坐标系中,反比例函数 的图象上有A、B两点,它们的横坐标分别为2和4, 的面积为6,则 的值为( )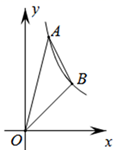 A、4 B、8 C、10 D、124. 如图,在中, , , 为边上的一点,且.若的面积为 , 则的面积为( )
A、4 B、8 C、10 D、124. 如图,在中, , , 为边上的一点,且.若的面积为 , 则的面积为( )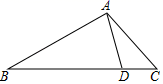 A、 B、 C、 D、5. 如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若
A、 B、 C、 D、5. 如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若 AOC=80°,则
AOC=80°,则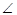 ADB的度数为( )
ADB的度数为( )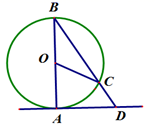 A、40° B、50° C、60° D、20°6. 抛物线y=ax2+bx+c如图所示,下列结论中正确的有( )
A、40° B、50° C、60° D、20°6. 抛物线y=ax2+bx+c如图所示,下列结论中正确的有( )①abc>0 ②b2-4ac<0 ③9a+3b+c<0 ④(a+c)2<b2⑤a+b<m(am+b)(其中m是不等于1的实数)
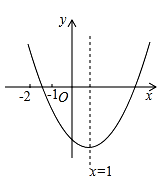 A、1个 B、2个 C、3个 D、4个7. 如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( )
A、1个 B、2个 C、3个 D、4个7. 如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( ) A、(2,3) B、(2,4) C、(3,3) D、(3,4)8. 在平面直角坐标系中,如果点P的横坐标与纵坐标相等,则称点P为和谐点,例如:点P(1,1)、(﹣2,﹣2)、(0.5,0.5)…,都是和谐点,若二次函数y=ax2+7x+c(a≠0)的图象上有且只有一个和谐点(﹣1,﹣1),则此二次函数的解析式为( )A、y=3x2+7x+3 B、y=2x2+7x+4 C、y=x2+7x+5 D、y=4x2+7x+29. 如图,在四边形ABCD中,BC∥AD,∠ADC=90°,点E沿着A→B→C的路径以2cm/s的速度匀速运动,到达点C停止运动,EF始终与直线AB保持垂直,与AD或DC交于点F,记线段EF的长度为dcm,d与时间t的关系图如图所示,则图中a的值为( )
A、(2,3) B、(2,4) C、(3,3) D、(3,4)8. 在平面直角坐标系中,如果点P的横坐标与纵坐标相等,则称点P为和谐点,例如:点P(1,1)、(﹣2,﹣2)、(0.5,0.5)…,都是和谐点,若二次函数y=ax2+7x+c(a≠0)的图象上有且只有一个和谐点(﹣1,﹣1),则此二次函数的解析式为( )A、y=3x2+7x+3 B、y=2x2+7x+4 C、y=x2+7x+5 D、y=4x2+7x+29. 如图,在四边形ABCD中,BC∥AD,∠ADC=90°,点E沿着A→B→C的路径以2cm/s的速度匀速运动,到达点C停止运动,EF始终与直线AB保持垂直,与AD或DC交于点F,记线段EF的长度为dcm,d与时间t的关系图如图所示,则图中a的值为( )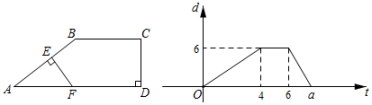 A、7.5 B、7.8 C、9 D、9.6
A、7.5 B、7.8 C、9 D、9.6二、填空题
-
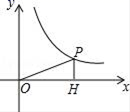
10. 已知点A(2,3)在反比例函数的图象上,当x>-2且x≠0时,则y的取值范围是.11. 已知一元二次方程x2-10x+21=0的两个根恰好分别是等腰三角形ABC的底边长和腰长,则△ABC的周长为 .12. 如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为.
 13. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果CD=4,那么AD•BD的值是.
13. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果CD=4,那么AD•BD的值是.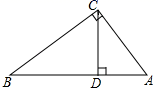 14. 有一人患了流感,经过两轮传染后共有64人患了流感,那么每轮传染中平均一个人传染给 个人.
14. 有一人患了流感,经过两轮传染后共有64人患了流感,那么每轮传染中平均一个人传染给 个人.
15. ⊙O的半径为1,弦AB= ,点C是圆上异于A、B的一动点,则∠ACB=.16. 如图,拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为米时,水面的宽度为米.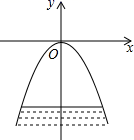 17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2020A2021=.
17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2020A2021=.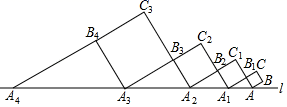
三、解答题
-
18. 计算或解方程:(1)、计算:(﹣1)0+(﹣)﹣1﹣2cos30°+;(2)、解方程:7x(5x+2)=6(5x+2).19. 已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
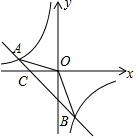 (1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,直接写出不等式kx+b﹣>0的解集.20. 已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,直接写出不等式kx+b﹣>0的解集.20. 已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°. (1)、求证:直线AD是⊙O的切线;(2)、若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
(1)、求证:直线AD是⊙O的切线;(2)、若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
21. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.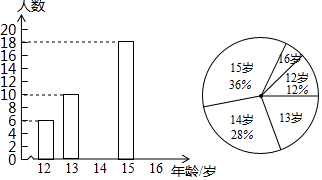
依据以上信息解答以下问题:
(1)、求样本容量,并补全条形统计图;(2)、直接写出样本的平均数,众数和中位数;(3)、若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.22. 如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).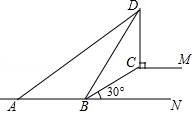 (1)、求灯杆CD的高度;(2)、求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)23. 某商店购进一批单价为30元的日用商品,如果以单价40元销售,那么每星期可售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.设销售单价为x(元)(x>40)时,该商品每星期获得的利润y(元).(1)、求出y与x之间的函数关系式及自变量x的取值范围;(2)、求出销售单价为多少元时,每星期获得的利润最大?最大利润是多少?24. 如图1,在△ABC中,AB=AC=10,tanB= , 点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)、求灯杆CD的高度;(2)、求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)23. 某商店购进一批单价为30元的日用商品,如果以单价40元销售,那么每星期可售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.设销售单价为x(元)(x>40)时,该商品每星期获得的利润y(元).(1)、求出y与x之间的函数关系式及自变量x的取值范围;(2)、求出销售单价为多少元时,每星期获得的利润最大?最大利润是多少?24. 如图1,在△ABC中,AB=AC=10,tanB= , 点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.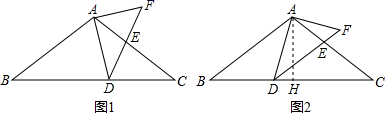 (1)、求证:△ABD∽△DCE;(2)、当AB∥DE时(如图2),求AE的长.(提示:过点A作AH⊥BC交BC于点H)25. 如图,抛物线与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)、求证:△ABD∽△DCE;(2)、当AB∥DE时(如图2),求AE的长.(提示:过点A作AH⊥BC交BC于点H)25. 如图,抛物线与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.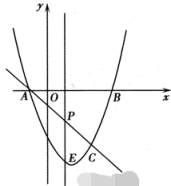 (1)、求A、B两点的坐标及直线AC的函数表达式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
(1)、求A、B两点的坐标及直线AC的函数表达式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.