湖南省娄底市新化县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
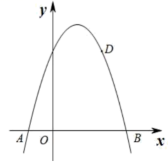
1. 反比例函数的比例系数是( )A、-3 B、3 C、 D、2. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、3. 已知四个非零实数a,b,c,d成比例,即 , 下列各式中不一定成立的是( )A、 B、 C、 D、4. 在平面直角坐标系内有一点 , 连接 , 则与x轴正方向所夹锐角的正弦值是( )A、 B、 C、 D、5. 若一组数据3、4、5、x、6、7的平均数是5,则x的值是( )A、4 B、5 C、6 D、76. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线7. 如图,为⊙O的直径,点C、D是的三等分点, , 则的度数为( )
 A、40° B、60° C、80° D、120°8. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根9. 如图▱ABCD,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则=( )
A、40° B、60° C、80° D、120°8. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根9. 如图▱ABCD,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则=( ) A、2:3 B、3:2 C、9:4 D、4:910. 如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC= , 则BC的长是( )
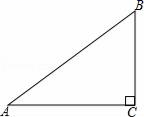
A、2:3 B、3:2 C、9:4 D、4:910. 如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC= , 则BC的长是( ) A、10 B、8 C、4 D、211. 已知关于x的一元二次方程的两个实数根为 , , 且 , 则k的值是( )A、4 B、5 C、6 D、712. 已知二次函数(a>0)的图象经过点A(−1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )A、c<3 B、m≤ C、n≤2 D、b<1
A、10 B、8 C、4 D、211. 已知关于x的一元二次方程的两个实数根为 , , 且 , 则k的值是( )A、4 B、5 C、6 D、712. 已知二次函数(a>0)的图象经过点A(−1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )A、c<3 B、m≤ C、n≤2 D、b<1二、填空题
-
13. 二次函数的顶点坐标是.14. 小华5次射击的成绩如下:(单位:环)5,9,7,10,9.其方差为3.2,如果他再射击1次,命中8环,那么他的射击成绩的方差 .(填“变大”、“变小”或“不变”)15. 七边形位似于七边形 , 它们的面积比为4∶9,已知位似中心O到A的距离为6,那么O到的距离为.16. 如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他每向前走60m,他的高度就升高36m,则这个斜坡的坡度等于.
 17. 如图,是⊙O的直径,C是⊙O上一点,于点D, , , 则的长为.
17. 如图,是⊙O的直径,C是⊙O上一点,于点D, , , 则的长为. 18. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG= , 则k=.
18. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG= , 则k=.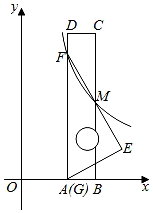
三、解答题
-
19. 计算:.20. 如图,的三个顶点都在⊙O上,直径 , .求的长.
 21. 某单位准备将院内一块长30m、宽20m的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示.要使种植花草的面积为532 , 那么小道进出口的宽应为多少米?(注:所有小道进出口的宽度相等)
21. 某单位准备将院内一块长30m、宽20m的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示.要使种植花草的面积为532 , 那么小道进出口的宽应为多少米?(注:所有小道进出口的宽度相等) 22. 为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
22. 为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:时间段
(小时/周)
小丽抽样
人数
小杰抽样
人数
0~1
6
22
1~2
10
10
2~3
16
6
3~4
8
2
(每组可含最低值,不含最高值)
 (1)、你认为哪位同学抽取的样本不合理?请说明理由;(2)、根据合理抽取的样本,把上图中的频数分布直方图补画完整;(3)、专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?23. 如图,为锐角三角形,是边上的高,正方形的一边在上,顶点G,H分别在 , 上,已知 , .
(1)、你认为哪位同学抽取的样本不合理?请说明理由;(2)、根据合理抽取的样本,把上图中的频数分布直方图补画完整;(3)、专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?23. 如图,为锐角三角形,是边上的高,正方形的一边在上,顶点G,H分别在 , 上,已知 , . (1)、求证:;(2)、求正方形的面积24. 如图1是自动卸货汽车卸货时的状态图,图2是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方,AB与水平线AD之间的夹角是5°,卸货时,车厢与水平线AD成60°,此时AB与支撑顶杆BC的夹角为45°,若AC=2米,求BC的长度.(结果保留一位小数)
(1)、求证:;(2)、求正方形的面积24. 如图1是自动卸货汽车卸货时的状态图,图2是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方,AB与水平线AD之间的夹角是5°,卸货时,车厢与水平线AD成60°,此时AB与支撑顶杆BC的夹角为45°,若AC=2米,求BC的长度.(结果保留一位小数)
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41)