湖南省娄底市娄星区2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关系式中，y是x的反比例函数的是（）

A、y＝3x B、y＝5x＋1 C、 $y = - x^{- 1}$ D、y＝x²﹣3

查看试题解析
2. 已知 $x = - 1$ 是关于 $x$ 的一元二次方程 $x^{2} + k x - 2 = 0$ 的一个根，则 $k$ 的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
3. 用配方法解方程x²﹣2x﹣2=0时，原方程应变形为（）

A、(x+1)²=3 B、(x+2)²=6 C、(x﹣1)²=3 D、(x﹣2)²=6

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(- 2 ， - 1)$ ，则该反比例函数的图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
5. 已知sin42°≈ $\frac{2}{3}$ ，则cos48°的值约为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{3}{2}$ D、 $- \frac{2}{3}$

查看试题解析
6. 已知在Rt△ABC中，∠C=90°，sinA= $\frac{3}{5}$ ，则∠A的正切值为（）

A、 $\frac{4}{3}$ B、 $\frac{4}{5}$ C、 $\frac{5}{4}$ D、 $\frac{3}{4}$

查看试题解析
7. 图形中，每个小网格均为正方形网格，带阴影部分的三角形中与如图△A₁B₁C₁相似的是（）

A、 B、 C、 D、

查看试题解析
8. 在第60届国际数学奥林匹克比赛中，中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为： $S^{2} = \frac{1}{6} [{(x_{1} - 38)}^{2} + {(x_{2} - 38)}^{2} + ⋯ + {(x_{6} - 38)}^{2}]$ ，下列说法错误的是（）.

A、我国一共派出了6名选手 B、我国参赛选手的平均成绩为38分 C、我国选手比赛成绩的中位数为38 D、我国选手比赛成绩的团体总分为228分

查看试题解析
9. 将抛物线 $y = 2 x^{2}$ 的图象先向右平移4个单位，再向下平移3个单位所得的解析式为（）

A、 $y = 2 {(x - 3)}^{2} + 4$ B、 $y = 2 {(x + 4)}^{2} - 3$ C、 $y = 2 {(x - 4)}^{2} + 3$ D、 $y = 2 {(x - 4)}^{2} - 3$

查看试题解析
10. 如图， $△ A B C$ 和 $△ A_{1} B_{1} C_{1}$ 是以点 $O$ 为位似中心的位似三角形，若 $C_{1}$ 为 $O C$ 的中点， $S_{△ A_{1} B_{1} C_{1}} = 3$ ，则 $△ A B C$ 的面积为（）

A、15 B、12 C、9 D、6

查看试题解析
11. 如图.AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（）

A、 $\frac{A D}{D F} = \frac{B C}{C E}$ B、 $\frac{A G}{G D} = \frac{B G}{C G}$ C、 $\frac{G C}{G E} = \frac{C D}{E F}$ D、 $\frac{A B}{E F} = \frac{A G}{G E}$

查看试题解析
12. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $(4 ， 0)$ ，其对称轴为直线 $x = 1$ ，结合图象给出下列结论：
① $a b c < 0$ ；② $4 a - 2 b + c > 0$ ；③当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大；④关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等实数根；⑤当 $- 2 < x < 4$ 时， $y > 0$ 其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 有一组数：x₁ ， x₂ ， x₃…x₁₀ ，若这组数的前4个数的平均数为12，后6个数的平均数为15，则这组数的平均数为.

查看试题解析
14. 已知关于x的方程 $m x^{2} - 3 x + 2 = 0$ 有两个实数根，那么m的取值范围是.

查看试题解析
15. 某斜坡的坡度 $i = \sqrt{3} : 3$ ，则它的坡角是度．

查看试题解析
16. 如图所示为抛物线y＝ax²＋2ax﹣3的图象，则一元二次方程ax²＋2ax﹣3＝0的两根为.

查看试题解析
17. 如图，直线 $A B$ 过原点分别交反比例函数 $y = \frac{6}{x}$ ，于A．B，过点A作 $A C ⊥ x$ 轴，垂足为C，则△ $A B C$ 的面积为．

查看试题解析
18. 符合黄金分割比例形式的图形很容易使人产生视觉上的美感.如图所示的五角星中，AD＝BC，且C、D两点都是AB的黄金分割点，若CD＝1，则AB的长是.

查看试题解析

三、解答题

19. 计算： $\sqrt{18} + (\frac{1}{2})^{- 1} - 6 s i n 4 5^{°} + (- π)^{0}$ .

查看试题解析
20. 某区为了了解初中学生毕业后的就读意向，对该区九年级部分学生进行了一次抽样调查，调查表设计有四个选项：A.只愿意就读普通高中；B.只愿意就读中等职业技术学校；C.就读普通高中或中等职业技术学校都愿意；D.其它.将调查数据进行了整理，并绘制了尚不完整的两幅统计图，请根据相关信息，解答下列问题：

(1)、本次活动共调查了多少名学生？

(2)、补全图①，并求出图②中A区域的圆心角的度数；

(3)、若该区九年级学生共有8000名，请估算该区九年级学生中只愿意就读普通高中的人数是多少？

查看试题解析
21. 热气球的探测器显示，从热气球看一栋高楼顶部的仰角为 $30 °$ ，看这栋高楼底部的俯角为 $60 °$ ，热气球与高楼的水平距离为66m，这栋高楼有多高？（结果精确到0.1m，参考数据： $\sqrt{3} \approx 1.73$ ）

查看试题解析
22. 如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．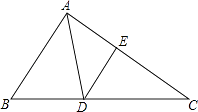

(1)、求证：△DCE∽△BCA；

(2)、若AB=3，AC=4．求DE的长．

查看试题解析
23. 山水旅行社的一则广告如下：我社组团去A风景区旅游，收费标准为：如果人数不超过30人，人均旅游费用为800元；如果人数多于30人，那么每增加1人，人均旅游费用降低10元，但人均旅游费用不得低于500元，某公司组织一批员工到A风景区旅游，支付给旅行社28000元.

(1)、该公司的人数_30人（填“大于、小于或等于”）

(2)、如果设该公司的人数为x，用含x的代数式表示人均旅游费用_（填化简结果）

(3)、求（2）中的x.

查看试题解析
24. 如图，在平面直角坐标系中，直线AB与y轴交于点B（0，5），与反比例函数y＝ $\frac{- 6}{x}$ 在第二象限内的图象相交于点A（﹣1，a）.

(1)、求直线AB的解析式；

(2)、将直线AB向下平移6个单位后与反比例函数的图象交于点C和点E，与y轴交于点D，求△ACD的面积；

(3)、设直线CD的解析式为y＝mx＋n，根据图象直接写出不等式mx＋n≤ $\frac{- 6}{x}$ 的解集.

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，AB＝10cm，sinA＝ $\frac{3}{5}$ .如果点P由B出发沿BA向点A匀速运动，同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s，点Q的速度为1cm/s.连接PQ，设运动时间为t（单位：s）（0≤t≤5）.

(1)、求AC，BC的长；

(2)、当t为何值时，△APQ与△ABC相似.

查看试题解析
26. 如图，已知二次函数y＝ax²＋bx＋c（a≠0）与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，直线y＝﹣2x＋3经过点C，与x轴交于点D.

(1)、求二次函数的解析式；

(2)、点P是（1）中的抛物线上的一个动点，设点P的横坐标为t（0＜t＜3），求△PCD的面积的最大值及此时点P的坐标.

查看试题解析