湖南省怀化市会同县2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下式中表示 $y$ 是 $x$ 的反比例函数的是（）

A、 $y = - x - 4$ B、 $y = x^{2}$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{5}{3 x}$

查看试题解析
2. 小明乘车从县城到怀化，行车的速度 $v (k m / h)$ 和行车时间 $t (h)$ 之间函数图是（）

A、 B、 C、 D、

查看试题解析
3. 若 $x_{1} + x_{2} = 3$ ， $x_{1}^{2} + x_{2}^{2} = 5$ ，则以 $x_{1}$ ， $x_{2}$ 为根的一元二次方程是（）

A、 $x^{2} - 3 x + 2 = 0$ B、 $x^{2} + 3 x - 2 = 0$ C、 $x^{2} + 3 x + 2 = 0$ D、 $x^{2} - 3 x - 2 = 0$

查看试题解析
4. 请你判断， $x | x | - 3 | x | + 2 = 0$ 的实根的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 一个两位数等于其各数位上数字的积的3倍，且个位上的数比十位上的数字大2，则这个两位数是（）

A、24 B、35 C、42 D、53

查看试题解析
6. 已知 $△ A B C$ 的三边长是 $\sqrt{2}$ ， $\sqrt{6}$ ， 2，则与 $△ A B C$ 相似的三角形的三边长可能是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、1， $\sqrt{3}$ ， $\frac{\sqrt{2}}{2}$ C、1， $\sqrt{3}$ ， $\frac{\sqrt{6}}{2}$ D、1， $\sqrt{3}$ ， $\frac{\sqrt{3}}{3}$

查看试题解析
7. 如图，△ $A B O$ ∽△ $C D O$ ，若 $B O = 6$ ， $D O = 3$ ， $C D = 2$ ，则 $A B$ 的长是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 若一元二次方程x²﹣2x﹣m＝0无实数根，则反比例函数y＝ $\frac{m + 1}{x}$ 的图象所在的象限是（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
9. 2sin45°的值等于（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
10. 某工厂从20万件的同类产品中随机抽取了100件进行质检，发现其中有5件不合格，那么估计该厂这20万件产品中合格品为（）件.

A、1万 B、19万 C、15万 D、20万

查看试题解析

二、填空题

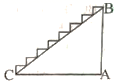
11. 某县校服生产有甲、乙、丙三种方案，为了了解何种图案更受欢迎，随机调查了某校学生100名，其中有60位学生喜欢甲方案，若该校有学生3000名，根据你所学的统计知识，估计该校喜欢甲方案的学生有人.

查看试题解析
12. 一元二次方程 $x^{2} - 2 x = 1$ 的两根 $α$ 、 $β$ ，则 $α + β + α \cdot β =$ .

查看试题解析
13. 已知 $\frac{a - 3 b}{2 a + b} = 3$ ，则 $\frac{6 b - 2 a}{6 a + 3 b} =$ .

查看试题解析
14. 某楼梯的侧面如所述，测得 $A C = 4 m$ ， $∠ A C B = 30 °$ ，则该楼梯的高度 $A B =$ .

查看试题解析
15. 点 $P (1, 1)$ 向左平移两个单位后恰好位于双曲线 $y = \frac{k}{x}$ 上，则 $k =$ ．

查看试题解析
16. 已知 $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ ，则 $\frac{2 x + 3 y - z}{y} =$ .

查看试题解析

三、解答题

17. 解方程.

(1)、 $3 x^{2} - 7 x = 0$

(2)、 $x^{2} + 4 x = 2$

查看试题解析
18. 计算 $3 t a n 30 ° - \frac{1}{c o s 60 °} + \sqrt{8} s i n 45 ° + \sqrt{{(1 - t a n 60 °)}^{2}}$ .

查看试题解析
19. 已知关于 $x$ 的一元二次方程 $a x^{2} + b x + \frac{1}{2} = 0$ .

(1)、若 $x = 1$ 是方程的一个解，写出 $a$ ， $b$ 满足的关系式？

(2)、当 $b = 1$ 时，利用根的判别式判断方程根的情况.

(3)、若方程有两个相等的实根，请写出一组满足条件的 $a$ ， $b$ 的值，并求出此时的方程根.

查看试题解析
20. 若AE与BD相交于点C.AC=3，BC=6，CD=10，CE=5，证明AB∥DE.

查看试题解析
21. 一艘船以40km/s的速度向正东航行，在A处测得灯塔C在北偏东60°方向上继续航行1h.到达B处，这时测得灯塔C在北偏东30°方向上，已知在灯塔C的四周30 km内有暗礁，问这船继续向东航行是否安全？

查看试题解析
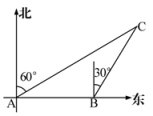22. 如图，在△ABC中，点D、E分别在边AB、BC上，AE与CD交于点F ，若AE平分∠BAC ， AB•AF＝AC•AE ．

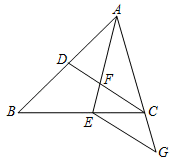(1)、求证：∠AFD＝∠AEC；

(2)、若EG∥CD ，交边AC的延长线于点G ，求证：CD•CG＝FC•BD ．

查看试题解析
23. 如图在 $10 \times 6$ 的正方形的网格中，每个小正方形的边长为1，线段 $A B$ 、 $E F$ 的端点均在小正方形的顶点上.

⑴在图中的 $A B$ 为边画 $R t △ A B C$ ，使点 $C$ 在小正方形的顶点上， $∠ B A C = 90 °$ 且 $t a n ∠ A C B = \frac{2}{3}$ .

⑵在（1）的条件下，在图中的以 $E F$ 为边画面积为3的 $△ D E F$ 使点 $D$ 在小正方形的顶点上， $∠ C B D = 45 °$ ，连结 $C D$ 直接写出线段 $C D$ 的长.

查看试题解析
24. 为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车
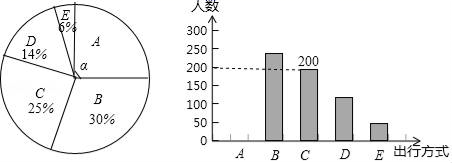
根据以上信息，回答下列问题：

(1)、参与本次问卷调查的市民共有_人，其中选择B类的人数有_人；

(2)、在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；

(3)、该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数.

查看试题解析
25. 如图1，AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线，过点A作AE⊥AD，交BD的延长线于点E.

(1)、求证：∠E= $\frac{1}{2}$ ∠C；

(2)、如图2，如果AE=AB，且BD：DE=2：3，求cos∠ABC的值；

(3)、如果∠ABC是锐角，且△ABC与△ADE相似，求∠ABC的度数.

查看试题解析

种类	A	B	C	D	E
出行方式	共享单车	步行	公交车	的士	私家车