湖南省常德市汉寿县2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，是二次函数的是（）

A、 $y = \frac{2}{x^{2}}$ B、 $y = \frac{3}{x}$ C、y＝x²+2x﹣1 D、y＝x﹣2

查看试题解析
2. 若x＝1是方程x²﹣3x+2a＝0的一个根，则（）

A、a＝﹣1 B、a＝﹣2 C、a＝1 D、a＝2

查看试题解析
3. 反比例函数 $y = \frac{m - 1}{x}$ 的图象在第一、第三象限，则m可能取的一个值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
4. 已知一组数据 $x_{1} ， x_{2} ， x_{3}$ 的平均数为3，则数据 $x_{1} + 2 ， x_{2} + 2 ， x_{3} + 2$ 的平均数是（）

A、3 B、5 C、6 D、7

查看试题解析
5. 抛物线y＝(x﹣1)²+2可由y＝x²如何平移得到（）

A、先向右平移1个单位，再向下平移2个单位 B、先向右平移1个单位，再向上平移2个单位 C、先向左平移1个单位，再向下平移2个单位 D、先向左平移1个单位，再向上平移2个单位

查看试题解析
6. 小明同学是一位古诗文的爱好者，在学习了一元二次方程这一章后，改编了苏轼诗词《念奴娇·赤壁怀古》：“大江东去浪淘尽，千古风流人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿同．哪位学子算得快，多少年华数周瑜？”假设周瑜去世时年龄的十位数字是 $x$ ，则可列方程为（）

A、 $10 x + (x - 3) = {(x - 3)}^{2}$ B、 $10 (x + 3) + x = x^{2}$ C、 $10 x + (x + 3) = {(x + 3)}^{2}$ D、 $10 (x + 3) + x = {(x + 3)}^{2}$

查看试题解析
7. 已知二次函 $y = {(x -1)}^{2} + h$ ， $(0 ， y_{1}) ， (2 ， y_{2}) ， (3 ， y_{3})$ 为其上面的点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁＝y₂＜y₃ B、y₁＜y₂＜y₃ C、y₁＜y₂＝y₃ D、y₃＜y₁＝y₂

查看试题解析
8. 如图，在△ABC中，∠BAC＝120°，AC＝8，AB＝4，则BC的长是（）

A、 $4 \sqrt{3}$ B、 $4 \sqrt{7}$ C、6 D、8

查看试题解析

二、填空题

9. 二次函数y＝﹣x²+4x+4的图象的顶点坐标为.

查看试题解析
10. 计算：2cos60°﹣sin30°+tan²45°＝.

查看试题解析
11. 下列y关于x的函数中，y随x的增大而增大的有.（填序号）
①y＝﹣x，②y＝x﹣1，③y＝(x﹣1)²（x＜0），④ $y = \frac{3}{x}$ .

查看试题解析
12. 如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为（1，2），点E的坐标为 $(- \frac{1}{2} ， 1)$ ，则点P的坐标为.

查看试题解析
13. 设m，n是一元二次方程x²+6x﹣7＝0的两个根，则m+n＝.

查看试题解析
14. 学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO＝6m，AB＝1.2m，CO＝1m，则栏杆C端应下降的垂直距离CD为m.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，如果CD＝ $\sqrt{3}$ ，那么AD•BD的值是.

查看试题解析
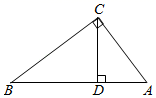16. 如图，矩形OABC的面积为18，对角线OB与双曲线y＝ $\frac{k}{x}$ （k＞0，x＞0）相交于点D，且OB：OD＝3：2，则k的值为.

查看试题解析

三、解答题

17. 解方程：2x²﹣x﹣1＝0.

查看试题解析
18. 已知△ABC中，∠C=90°，AB=6，∠A=45°，求△ABC的面积.

查看试题解析
19. 已知二次函数y=ax²+bx+3的图象经过点 (－3，0)，(2，－5).

(1)、试确定此二次函数的解析式；

(2)、请你判断点P(－2，3)是否在这个二次函数的图象上？

查看试题解析
20. 如图，△ABC中，DE∥BC，EF∥AB.

(1)、求证：△ADE∽△EFC；

(2)、若AD＝4，DE＝6， $\frac{A E}{E C}$ ＝2，求EF和FC的值.

查看试题解析
21. 如图，一次函数y₁＝kx+b与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于A(2，3)，B(6，n)两点，与x轴、y轴分别交于C，D两点.

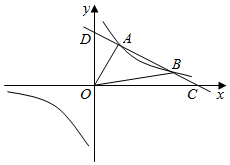(1)、求一次函数与反比例函数的解析式.

(2)、求当x为何值时，y₁＞y₂.

查看试题解析
22. 某校组织九年级学生体育健康抽测，（1）班25名学生的成绩统计如下：90，74，88，65，98，76，81，42，85，70，55，80，95，88，72，87，61，56，76，66，78，72，82，63，100.

(1)、90分及以上为A级，75～89分为B级，60～74分为C级，60分以下为D级.请把下面表格补充完整，并将图中的条形图补充完整；
等级
A
B
C
D
人数
            ▲
            ▲
8
            ▲

(2)、该校九年级共有1000名学生，如果75分以上为良好，请估计九年级有多少学生的成绩为良好？

(3)、请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.

查看试题解析
23. 清代《修武县志》有胜果寺的记载，“康熙五十二年三月十七日，塔顶现青白二气如云，越二日乃止”，此文中的塔即为“胜果寺塔”，是修武作为“千年古县”的标志性古建筑.为了测量塔的高度，某校数学兴趣小组的两名同学采用了如下方式进行测量.如图，小明站在 $A$ 处，眼睛 $E$ 距离地面的高度为 $1.85 m$ ，测得塔顶 $C$ 的仰角为 $45 °$ ，小红站在距离小明 $10 m$ 的 $D$ 处，眼睛 $F$ 距离地面的高度为 $1.5 m$ ，测得塔顶 $C$ 的仰角为 $60 °$ ，已知 $A$ ， $D$ ，塔底 $B$ 在同一水平面上，由此即可求出塔高 $B C$ .你知道是怎么求的吗？请写出解题过程.（结果精确到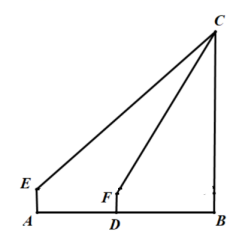 $1 m$ .参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 如图，某校广场有一段25米长的旧围栏，现打算利用该围栏的一部分（或全部）为一边，围成一块100平方米的长方形草坪（如图CDEF，CD＜CF）已知整修旧围栏的价格是每米1.75元，建新围栏的价格是4.5元.若CF＝x米，计划修建费为y元.

(1)、求y与x的函数关系式，并指出x的取值范围；

(2)、若计划修建费为150元，能否完成该草坪围栏的修建任务？若能完成，请算出利用旧围栏多少米；若不能完成，请说明理由.

查看试题解析
25. 如图，抛物线y＝－x²＋bx＋c与x轴相交于A（－1，0），B（5，0）两点.

(1)、求抛物线的解析式；

(2)、在第二象限内取一点C，作CD垂直x轴于点D，链接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；

(3)、在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点.试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请写出点Q的坐标；若不存在，请说明理由.

查看试题解析
26. 已知：如图，在Rt△ACB中，∠C=90°，BC=3cm，AC=3 $\sqrt{3}$ cm，点P由B点出发沿BA方向向点A匀速运动，速度为2cm/s；点Q由A点出发沿AC方向向点C匀速运动，速度为 $\sqrt{3}$ cm/s；若设运动的时间为t(s)(0＜t＜3)，解答下列问题：

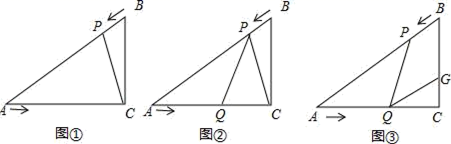(1)、如图①，连接PC，当t为何值时△APC∽△ACB，并说明理由；

(2)、如图②，当点P，Q运动时，是否存在某一时刻t，使得点P在线段QC的垂直平分线上，请说明理由；

(3)、如图③，当点P，Q运动时，线段BC上是否存在一点G，使得四边形PQGB为菱形？若存在，试求出BG长；若不存在请说明理由．

查看试题解析

等级	A	B	C	D
人数	▲	▲	8	▲