湖南省株洲市荷塘区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数﹣ $\frac{1}{6}$ ，0， $\sqrt{2}$ ，3.14中，无理数是（　　）

A、﹣ $\frac{1}{6}$ B、0 C、 $\sqrt{2}$ D、3.14

查看试题解析
2. 如果分式 $\frac{a^{2}}{a + b}$ 中的a，b都同时扩大2倍，那么该分式的值（）

A、不变 B、缩小2倍 C、扩大2倍 D、扩大4倍

查看试题解析
3. 若代数式 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥－3 B、x＞3 C、x≥3 D、x≤3

查看试题解析
4. 不等式组 ${\begin{array}{l} x \leq 4 \\ x > 2 \end{array}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
5. 据天气预报2018年4月12日大田县的最高气温是32℃，最低气温是21℃，则当天大田县气温t（℃）的变化范围是（）

A、t＞21 B、t＜32 C、21＜t＜32 D、21≤t≤32

查看试题解析
6. 若不等式组 ${\begin{array}{l} x < 1 \\ x < m \end{array}$ 的解为x＜m，则m的取值范围为（）

A、m≤1 B、m=1 C、m≥1 D、m＜1

查看试题解析
7. 下列说法错误的是（）

A、1的平方根是1 B、 $- 1$ 的立方根是 $- 1$ C、 $\sqrt{2}$ 是2的平方根 D、 $- \sqrt{3}$ 是 $\sqrt{{(- \sqrt{3})}^{2}}$ 的平方根

查看试题解析
8. 如图，AD是△ABC的中线，△ABD比△ACD的周长大6 cm，则AB与AC的差为（）

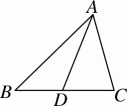A、2 cm B、3 cm C、6 cm D、12 cm

查看试题解析
9. 若a、b是等腰三角形ABC的两条边，且 $\sqrt{a - 3} + | b - 6 | = 0$ ，则 $△ A B C$ 的周长为（　　）

A、12 B、12和15 C、9和12 D、15

查看试题解析
10. $\sqrt{16}$ 的平方根是（　　）

A、±4 B、4 C、±2 D、2

查看试题解析

二、填空题

11. 当x=1时，分式 $\frac{x}{x + 2}$ 的值是．

查看试题解析
12. 如图，小雨把不等式3x+1＞2（x﹣1）的解集表示在数轴上，则阴影部分盖住的数字是.

查看试题解析
13. 如图，两个三角形全等，则∠α的度数是

查看试题解析
14. 比较大小： $\sqrt{7}$ 3（填写“＜”或“＞”）．

查看试题解析
15. 如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是（只写一个条件即可）.

查看试题解析
16. $\sqrt{{(3 - π)}^{2}} =$ ．

查看试题解析
17. 如图，AB∥CD，AD∥BC，OE=OF，图中全等三角形共有对.

查看试题解析
18. 观察下列各式： $\sqrt{1 + \frac{1}{3}}$ =2 $\sqrt{\frac{1}{3}}$ ； $\sqrt{2 + \frac{1}{4}}$ =3 $\sqrt{\frac{1}{4}}$ ； $\sqrt{3 + \frac{1}{5}}$ =4 $\sqrt{\frac{1}{5}}$ ，……请你将发现的规律用含自然数n（n≥1）的等式表示出来．

查看试题解析

三、解答题

19. 计算 $- 2^{2} + \sqrt{16} - 2 \times \sqrt{{(- 3)}^{2}}$ ．

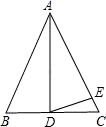
查看试题解析
20. 若关于x的不等式组 ${\begin{array}{l} x - a \geq 0 \\ 3 - 2 x > - 1 \end{array}$ 的整数解恰有5个，求a的范围.

查看试题解析
21. 如图，在△ABC中，AB＝AC，AD⊥BC，∠BAD＝28°，且AD＝AE，求∠EDC的度数．

查看试题解析
22. 已知T= $(\frac{x + 1}{x^{2} - 1} - \frac{1}{1 - x}) \div \frac{x + 2}{x^{2} - x}$ ，

(1)、化简T；

(2)、若正方形ABCD的边长为 $x$ ，且它的面积为4，求T的值.

查看试题解析
23. 如图，四边形ABCD中，AB∥CD，∠A＝60°，

(1)、作∠ADC的角平分线DE，交AB于点E；(要求：尺规作图，保留作图痕迹，不必写作法和证明)；

(2)、判断△ADE是什么三角形，并说明理由；

查看试题解析
24. 某县为落实“精准扶贫惠民政策"，计划将某村的居民自来水管道进行改造该工程若由甲队单独施工，则恰好在规定时间内完成；若由乙队单独施工，则完成工程所需天数是规定时间的1.5倍；若由甲、乙两队先合作施工15天，则余下的工程由甲队单独完成还需5天这项工程的规定时间是多少天？

查看试题解析
25. 在进行二次根式的化简与运算时，如遇到 $\frac{3}{\sqrt{5}}$ ， $\sqrt{\frac{2}{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，还需做进一步的化简：
$\frac{3}{\sqrt{5}}$ = $\frac{3 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}}$ = $\frac{3 \sqrt{5}}{5}$ .①
$\sqrt{\frac{2}{3}}$ = $\sqrt{\frac{2 \times 3}{3 \times 3}}$ = $\frac{\sqrt{6}}{3}$ .②
$\frac{2}{\sqrt{3} + 1}$ = $\frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)}$ = $\frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}}$ = $\sqrt{3}$ ﹣1.③
以上化简的步骤叫做分母有理化.
$\frac{2}{\sqrt{3} + 1}$ 还可以用以下方法化简：
$\frac{2}{\sqrt{3} + 1}$ = $\frac{3 - 1}{\sqrt{3} + 1}$ = $\frac{{(\sqrt{3})}^{2} - 1}{\sqrt{3} + 1}$ = $\frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1}$ = $\sqrt{3}$ ﹣1.④

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ .
（I）参照③式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ =；
（II）参照④式化简 $\frac{2}{\sqrt{5} + \sqrt{3}} =$ ；

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + . . . . . . + \frac{1}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$ .

查看试题解析
26. 如图，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：

(1)、PC＝cm.（用t的代数式表示）

(2)、当t为何值时，△ABP≌△DCP？

(3)、当点P从点B开始运动，同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由.

查看试题解析