湖南省长沙市宁乡市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，是分式的是（）

A、 $x$ B、 $\frac{x}{x + 2}$ C、 $\frac{x}{π}$ D、 $\frac{x}{2} + 1$

查看试题解析
2. 如图，在 $△ A B C$ 中， $A B$ 边上的高为（）

A、 $C G$ B、 $B F$ C、 $B E$ D、 $A D$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} - b^{2} = (a - b)^{2}$ B、 $a^{3} + b^{4} = a^{7}$ C、 $a^{8} \div a^{2} = a^{4}$ D、 $a^{3} \cdot a^{2} = a^{5}$

查看试题解析
4. 如图，阴影部分是由5个小正方形涂黑组成的一个直角图形，再将方格内空白的两个小正方形涂黑，得到新的图形（阴影部分），其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 计算 $\sqrt{5} \times \sqrt{10}$ 的结果为（）

A、 $10 \sqrt{5}$ B、 $5 \sqrt{2}$ C、 $3 \sqrt{2}$ D、 $2 \sqrt{5}$

查看试题解析
6. 一副三角板按如图所示方式叠放在一起，则图中∠ $α$ 等于（）

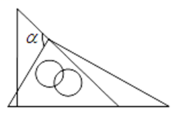A、105° B、115° C、120° D、125°

查看试题解析
7. 如图，△ $A B E$ ≌△ $A C F$ ，且 $A C = 10 ， A F = 4$ ，则 $B F$ 的长为（）

A、5 B、6 C、7 D、8

查看试题解析
8. 下列说法：①全等的两个图形一定成轴对称；②成轴对称的两个图形一定全等③轴对称图形的对称点一定在对称轴的两侧；④若点A、B关于直线MN对称，则直线MN垂直平分线段AB.正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知 $(a - b)^{2} = 6 ， (a + b)^{2} = 4$ ，则 $a^{2} + b^{2}$ 的值（）

A、10 B、6 C、5 D、3

查看试题解析
10. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为 $a ， b ， c$ ，则该三角形的面积为 $S = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ ，现已知∆ $A B C$ 的三边长分别为 $2 ， 3 ， 4$ ，则∆ $A B C$ 的面积为（）

A、 $\frac{3 \sqrt{15}}{4}$ B、 $\frac{3 \sqrt{15}}{8}$ C、 $\frac{3 \sqrt{15}}{2}$ D、 $\frac{\sqrt{15}}{2}$

查看试题解析
11. 定义运算“⊙”： $a ⊙ b = {\begin{array}{l} \frac{a}{a - b} (a > b) \\ \frac{b}{b - a} (a < b) \end{array}$ ，若 $5 ⊙ x = 2$ ，则 $x$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{5}{2}$ 或10 C、10 D、 $\frac{5}{2}$ 或 $\frac{15}{2}$

查看试题解析
12. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（）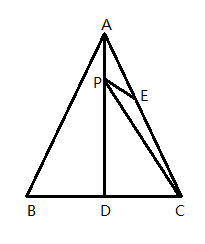

A、30° B、45° C、60° D、90°

查看试题解析

二、填空题

13. 二次根式 $\sqrt{2 - 3 x}$ 有意义，则x的取值范围是

查看试题解析
14. 点 $(3 + a ， 5)$ 关于 $y$ 轴对称的点的坐标是 $(- 5 ， 4 - b)$ ，则 $b^{a} =$ ．

查看试题解析
15. 如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为 1800°的新多边形，则原多边形的边数为.

查看试题解析
16. 在△ABC中,∠C=90°,BC=16cm,∠BAC的平分线交BC于点D,且BD∶DC=5∶3,则D到AB的距离为cm.

查看试题解析
17. 若分式 $\frac{| x | - 3}{(x - 3) (x + 2)}$ 的值为0，则 $x$ ＝ .

查看试题解析
18. 如图所示，已知 $A B = C D = a$ ， $B C = D E = E F = F G = G H = b$ ，根据图形把多项式 $a^{2} + 5 a b + 4 b^{2}$ 因式分解所得的结果为.

查看试题解析

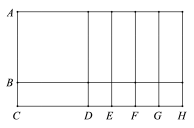
三、解答题

19. 计算：

(1)、 $3 a^{3} b \cdot (- 2 b)^{2} + (- a b) (2 a b)^{2}$

(2)、 $(2 x + 3 y) (5 x - 2 y)$

查看试题解析
20. 分解因式：

(1)、 $2 a^{2} - 8$

(2)、 $2 a x^{2} - 4 a x + 2 a$

查看试题解析
21. 已知 $x ， y$ 满足 $y < \sqrt{x - 3} - \sqrt{3 - x} + 5$ ，试化简 $| y - 5 | - \sqrt{y^{2} - 12 y + 36}$ .

查看试题解析
22. 先化简，再求值： $(1 - \frac{2}{x - 1}) \div \frac{x^{2} - 6 x + 9}{x - 1}$ ，请从0，1，2，3四个数中选取一个你喜欢的数 $x$ 代入求值.

查看试题解析
23. 如图，在长度为1个单位长度的小正方形组成的网格图中，点A、B、C在小正方形的顶点上.

(1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′；

(2)、三角形ABC的面积为；

(3)、在直线l上找一点P，使PB+PC的长最短.

查看试题解析
24. 近年来，雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置，需购进 $A ， B$ 两种设备.已知每台 $B$ 种设备比每台 $A$ 种设备价格多0.6万元，花5万元购买A种设备和花11万元购买B种设备的数量相同.

(1)、求 $A ， B$ 两种设备每台各多少万元.

(2)、根据单位实际情况，需购进 $A ， B$ 两种设备共18台，总费用不高于14万元.求 $A$ 种设备至少要购买多少台？

查看试题解析
25. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，请解答下列问题：

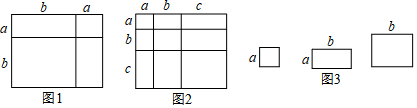(1)、写出图2中所表示的数学等式.

(2)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 8 ， a^{2} + b^{2} + c^{2} = 36$ ，求 $a b + b c + a c$ 的值.

(3)、小明同学用图 $3$ 中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形 $z$ 张边长分别为 $a ， b$ 的长方形纸片拼出一个面积为 $(4 a + 7 b) (6 a + 5 b)$ 长方形，求 $x + y + z$ 的值.

查看试题解析
26. 如图1，在边长为 $6$ 的等边∆ $A B C$ 中，点 $D$ 是边 $A B$ 上一个动点，过点 $D$ 作 $D E$ ⊥ $A C$ 于点 $E$ .

(1)、求证： $A E = \frac{1}{2} A D$ ；

(2)、如图2，过点 $D$ 向 $B C$ 引垂线交 $B C$ 于点 $F$ ，当 $D E = D F$ 时，试判断 $D$ 点在 $A B$ 上的位置，并说明理由；

(3)、如图3，延长 $B C$ 至 $G$ ，使 $C G = A D$ ，连接 $D G$ 交 $A C$ 于点 $H$ ，随着 $D$ 点的移动，请判断线段 $E H$ 的长度是否发生变化；若变化，请说明理由；若不变，请求出 $E H$ 的值.

查看试题解析