湖南省邵阳市新邵县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 在实数-2、、0、中,绝对值最大的实数是( )A、-2 B、 C、0 D、2. 若 , 则下列不等式变形正确的是( )A、 B、 C、 D、3. 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
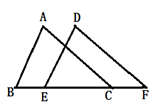 A、AC//DF B、∠A=∠D C、AC=DF D、BE=CF4. 代数式有意义,则的取值范围在数轴上表示正确的是( )A、
A、AC//DF B、∠A=∠D C、AC=DF D、BE=CF4. 代数式有意义,则的取值范围在数轴上表示正确的是( )A、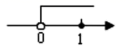 B、
B、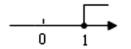 C、
C、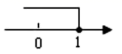 D、
D、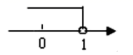 5. 下列命题,是真命题的是( )A、直角三角形的一个内角为32°,则另外一个锐角为68° B、如果 , 那么 C、有两边和一角对应相等的两个三角形全等 D、如果一个数的立方根等于这个数本身,那么这个数是0或6. 将一副三角板按如图所示的方式放置,则等于( )
5. 下列命题,是真命题的是( )A、直角三角形的一个内角为32°,则另外一个锐角为68° B、如果 , 那么 C、有两边和一角对应相等的两个三角形全等 D、如果一个数的立方根等于这个数本身,那么这个数是0或6. 将一副三角板按如图所示的方式放置,则等于( )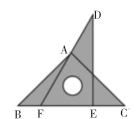 A、75° B、90° C、105° D、120°7. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 下列尺规作图,能判断AD是△ABC边上的高是( )A、
A、75° B、90° C、105° D、120°7. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 下列尺规作图,能判断AD是△ABC边上的高是( )A、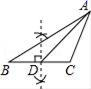 B、
B、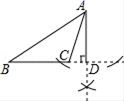 C、
C、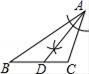 D、
D、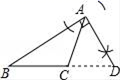 9. 如果 , , 那么下面各式不正确的是( )A、 B、 C、 D、10. 某工程需要在规定时间内完成,如果甲工程队单独做,恰好如期完成; 如果乙工程队单独做,则多用天,现在甲、乙两队合做天,剩下的由乙队单独做,恰好如期完成,求规定时间.如果设规定日期为天,下面所列方程中错误的是( )A、 B、 C、 D、
9. 如果 , , 那么下面各式不正确的是( )A、 B、 C、 D、10. 某工程需要在规定时间内完成,如果甲工程队单独做,恰好如期完成; 如果乙工程队单独做,则多用天,现在甲、乙两队合做天,剩下的由乙队单独做,恰好如期完成,求规定时间.如果设规定日期为天,下面所列方程中错误的是( )A、 B、 C、 D、二、填空题
-
11. 在实数范围内因式分解:2-4=.12. 2019新型冠状病毒(2019-nCoV),因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名.新型冠状病毒是以前从未在人体中发现的冠状病毒新毒株,它的直径约在 , 用科学记数法可表示为.13. 已知射线OM.以O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,如图所示,则∠AOB=(度)
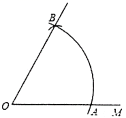 14. 计算: 的结果是 .15. 关于的分式方程有增根,则此分式方程的增根为.16. 如图,点、点分别是的边和的中点,若的面积是 , 则的面积为.
14. 计算: 的结果是 .15. 关于的分式方程有增根,则此分式方程的增根为.16. 如图,点、点分别是的边和的中点,若的面积是 , 则的面积为.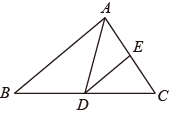 17. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式;也叫三斜求积公式,即如果一个三角形的三边长分别为 , , , 那么该三角形的面积为.已知的三边长分别为2,4, , 则的面积为.18. 已知关于 , 的方程组的解 , 都为正数,满足不等式成立的整数的值为(写一个即可).
17. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式;也叫三斜求积公式,即如果一个三角形的三边长分别为 , , , 那么该三角形的面积为.已知的三边长分别为2,4, , 则的面积为.18. 已知关于 , 的方程组的解 , 都为正数,满足不等式成立的整数的值为(写一个即可).三、解答题
-
19. 计算:20. 解不等式组 , 并求出不等式组的所有整数解.21. 先化简: , 再从的范围内选取一个你喜欢的值代入求值.22. 如图,在四边形中, , 为的中点,连接、 , , 延长交的延长线于点.
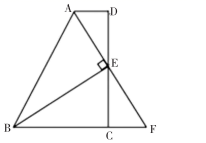 (1)、求证:;(2)、若 , , 求四边形的面积.23. 老师展示小明解方程的过程如下:
(1)、求证:;(2)、若 , , 求四边形的面积.23. 老师展示小明解方程的过程如下:解:方程两边同时乘以 , 得
解这个方程,得
检验:当时,
是原分式方程的解
同学们一眼就发现了他的解法有错误,你发现了吗?请你帮助小明写出正确的解答过程.
24. 2020年新冠肺炎疫情影响全球,各国感染人数持续攀升,医用口罩供不应求,很多企业纷纷加入生产口罩的大军中来,邵阳某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的1.5倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.(1)、求甲、乙两厂房每天各生产多少箱口罩;(2)、已知甲、乙两厂房生产这种口罩每天的生产费分别是1500元和1200元,现有30000箱口罩的生产任务,甲厂房单独生产一段时间后另有安排,剩余任务由乙厂房单独完成.如果总生产费不超过81000元,那么甲厂房至少生产了多少天?