湖南省怀化市会同县2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 某病毒近似于球体，它的平均直径是 $0.00000008 m$ ，用科学记数法记为（）

A、 $8 \times 1 0^{- 8}$ B、 $8 \times 1 0^{- 7}$ C、 $8 \times 1 0^{- 6}$ D、 $8 \times 1 0^{- 5}$

查看试题解析
2. 下列运算正确的是（）

A、 $- π^{0} = 1$ B、 ${(- 3)}^{- 1} = \frac{1}{3}$ C、 ${(- 2^{m - n})}^{2} = 4^{m - n}$ D、 ${(a + b)}^{- 1} = a^{- 1} + b^{- 1}$

查看试题解析
3. 三角形的下列线段中将三角形的面积分成相等两部分的是（）

A、中线 B、角平分线 C、高 D、以上都对

查看试题解析
4. 已知，如图在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是三角形的高，若 $∠ C A D = 20 °$ ，则 $∠ B$ 的度数是（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
5. 下列实数中，最大的数是（）

A、 $| - 4 |$ B、 $\sqrt{5}$ C、 $π$ D、 $\frac{11}{3}$

查看试题解析
6. 如图，数轴上点N表示的数可能是（）

A、 $\sqrt{10}$ B、 $\sqrt{7}$ C、 $\sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
7. 规定用符号 $[x]$ 表示一个实数的整数部分，如 $[2.04] = 2$ ， $[- 2.94] = - 2$ ，则 $[\sqrt{10} - 1] =$ （）

A、1 B、2 C、3 D、4

查看试题解析
8. 下列不等式中，变形错误的是（）

A、 $x > y$ 则 $x + 1 > y + 1$ B、若 $- a > - b$ 则 $a < b$ C、 $- \frac{1}{2} x > y$ 则 $x < - 2 y$ D、若 $- 3 x < 5$ 则 $x < - \frac{5}{3}$

查看试题解析
9. 下列根式中是最简二次根式是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{\frac{4}{7}}$ C、 $\sqrt{12}$ D、 $\sqrt{2}$

查看试题解析
10. 如图，分别以线段AB的两端点A，B为圆心，大于 $\frac{1}{2}$ AB长为半径画弧，在线段AB的两侧分别交于点E，F，作直线EF交AB于点O.在直线EF上任取一点P（不与O重合），连接PA，PB，则下列结论不一定成立的是（）

A、 $P A = P B$ B、 $O A = O B$ C、 $O P = O F$ D、 $P O ⊥ A B$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 3}$ 中，x的取值范围是．

查看试题解析
12. $\sqrt{16}$ 的算术平方根的相反数是．

查看试题解析
13. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $B C$ 边上的高，点 $E$ 、 $F$ 是 $A D$ 的三等分点，若 $△ A B C$ 的面积是 $S$ ，则图中阴影部分的面积是.

查看试题解析
14. 已知 $△ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ，则 $| a - b - c | + | b - c - a | + | c - a + b | =$ .

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 的中点， $D E ⊥ A C$ ，垂足为 $E$ ， $∠ B A C = 40 °$ ，则 $∠ A D E$ 的度数为.

查看试题解析
16. 如图，数轴上 $A$ 、 $B$ 两点所表示的数是 $- 4 \sqrt{3}$ 和 $\sqrt{3}$ 点 $C$ 是线段 $A B$ 的中点，则点 $C$ 所表示的数是.

查看试题解析

三、解答题

17. 计算：

(1)、 $(\sqrt{32} + \sqrt{2}) \div \sqrt{2}$

(2)、 $(3 + \sqrt{10}) (\sqrt{2} - \sqrt{5})$

(3)、 ${(π - 3.14)}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt[3]{27} - \sqrt{8}$

查看试题解析
18. 解不等式（或组）：

(1)、 $\frac{x}{3} + 2 + \frac{x}{4} \leq 9$

(2)、 ${\begin{array}{l} 4 x - 7 < 5 (x - 1) \\ \frac{x}{3} > 4 - \frac{x - 2}{2} \end{array}$

查看试题解析
19. 解方程：

(1)、 $\frac{x}{x - 1} - \frac{2}{x} = 1$

(2)、 $\frac{3 x - 1}{x + 2} = - 4$

查看试题解析
20. 先化简，再求值： $\frac{a - 1}{a^{2} - 2 a + 1} - \frac{a - 1}{a^{2} - 1}$ ，其中 $a = \sqrt{3}$ ．

查看试题解析
21. 如图，在梯形ABCD中，AD∥BC，E为CD中点，连接AE并延长AE交BC的延长线于点F．

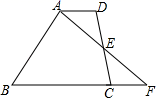(1)、求证：CF＝AD.

(2)、若AD＝3，AB＝8，当BC为多少时，点B在线段AF的垂直平分线上，为什么？

查看试题解析
22. 已知： ∠α，直线 $l$ 及 $l$ 上两点 A， B．
求作： Rt△ABC ，使点 C 在直线 $l$ 的上方，且∠ABC=90°， ∠BAC=∠α．

查看试题解析
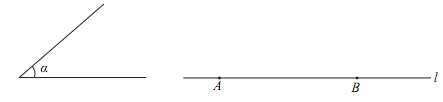23. 为响应国家“足球进校园”的号召，某校购买了50个A类足球和25个B类足球共花费7500元，已知购买一个B类足球比购买一个A类足球多花30元.

(1)、求购买一个A类足球和一个B类足球各需多少元？

(2)、通过全校师生的共同努力，今年该校被评为“足球特色学校”，学校计划用不超过4800元的经费再次购买A类足球和B类足球共50个，若单价不变，则本次至少可以购买多少个A类足球？

查看试题解析
24. 如图，在 $Δ A B C$ 中，D是 $B C$ 边上的一点， $A B = D B$ ， $B E$ 平分 $∠ A B C$ ，交 $A C$ 边于点E，连接 $D E$ .

(1)、求证： $Δ A B E ≅ Δ D B E$ ；

(2)、若 $∠ A = 100 °$ ， $∠ C = 50 °$ ，求 $∠ A E B$ 的度数.

查看试题解析
25. 数学家华罗庚在一次出国访问途中，看到飞机上的乘客阅读的杂志上有道智力题，求59319的立方根，华罗庚脱口而出“39”，邻座的乘客十分惊奇，忙问其中的奥妙.你知道怎样迅速的计算结果吗？请你按下面的结果试一试.
第一步： $∵ \sqrt[3]{1000} = 10$ ， $\sqrt[3]{1000000} = 100$
$1000 < 59319 < 1000000$ ， $∴ 10 < \sqrt[3]{59319} < 100$
它的立方根是一个两位数.
第二步： $∵ 59319$ 的个位数是9， $9^{3} = 729$ .
$∴$ 能确定 $\sqrt{59319}$ 的个位数是9.
第三步：如果划出59319后面的三位数，得到数59
而 $\sqrt[3]{27} < \sqrt[3]{59} < \sqrt[3]{64}$ ，可得 $30 < \sqrt[3]{59319} < 40$ .
由此确定59319的立方根的十位数是3， $∴$ 它的立方根是39.
[解答问题]
根据上面的材料解答下面的问题：

(1)、求110592的立方根，写出步骤.

(2)、填空： $\sqrt[3]{85184} =$ .

查看试题解析