重庆市酉阳土家族苗族自治县2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 的倒数是( )A、3 B、3 C、 D、2. 我县某山区学校去年秋季期末考试时最高气温为 , 最低气温为 , 那么这天的最高气温比最低气温高( )A、 B、 C、 D、3.
如图,矩形绕它的一条边MN所在的直线旋转一周形成的几何体是( )

A、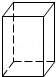 B、
B、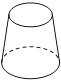 C、
C、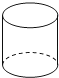 D、
D、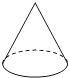 4. 下列各式从左到右的运算中,成立的是( )A、 B、 C、 D、5. 当时,关于的方程的解为( )A、 B、 C、 D、6. 下列说法正确的是( )A、是一次单项式 B、的系数是 C、的指数是 D、的系数是7. 如果 , 则代数式的值为( )A、 B、 C、 D、8. 若两个单项式与是同类项,则式子的值为( )A、 B、 C、 D、 或9. 某网店安踏牌运动鞋以a元的价格卖出,利润率为20%,则该运动鞋的成本为( )A、元 B、元 C、元 D、元10. 已知某点阵的第①②③个图如图所示,按此规律第⑥个点阵图中点的个数为( )
4. 下列各式从左到右的运算中,成立的是( )A、 B、 C、 D、5. 当时,关于的方程的解为( )A、 B、 C、 D、6. 下列说法正确的是( )A、是一次单项式 B、的系数是 C、的指数是 D、的系数是7. 如果 , 则代数式的值为( )A、 B、 C、 D、8. 若两个单项式与是同类项,则式子的值为( )A、 B、 C、 D、 或9. 某网店安踏牌运动鞋以a元的价格卖出,利润率为20%,则该运动鞋的成本为( )A、元 B、元 C、元 D、元10. 已知某点阵的第①②③个图如图所示,按此规律第⑥个点阵图中点的个数为( ) A、 B、 C、 D、11. 如图1是一个边长为的正方形纸片,将其剪去两个小长方形,得到一个宽度都为的“5字形”的图案如图2所示,再将剪下的两个小长方形拼成一个新的长方形如图3所示,则图3长方形的周长为( )
A、 B、 C、 D、11. 如图1是一个边长为的正方形纸片,将其剪去两个小长方形,得到一个宽度都为的“5字形”的图案如图2所示,再将剪下的两个小长方形拼成一个新的长方形如图3所示,则图3长方形的周长为( ) A、 B、 C、 D、12. 如图是一个时钟某一时刻的简易图,图中的条短线刻度位置是时钟整点时时针(短针)位置,根据图中时针和分针(长针)位置,该时钟显示时间是( )
A、 B、 C、 D、12. 如图是一个时钟某一时刻的简易图,图中的条短线刻度位置是时钟整点时时针(短针)位置,根据图中时针和分针(长针)位置,该时钟显示时间是( ) A、点 B、点 C、点 D、点
A、点 B、点 C、点 D、点二、填空题
-
13. 2020年6月28日这天,来自国内外的人参加了酉阳县举办的“2020重庆酉阳国际帐篷音乐节”活动,将5405用科学记数法表示为.14. 把多项式按的升幂排列为.15. 写出只含有字母的一个二次三项式.16. 刘明同学在解一元一次方程时,不小心把?处的系数弄得看不清了,他便问邻桌,但是邻桌只告诉他,该方程的解是(邻桌的答案是正确的),刘明同学便由此计算出了?处的系数,那么这个系数是.17. 如图所示,如果将图中各小正方形翻折起来得到一个正方体,那么“我”的对面是(填汉字)
 18. 已知条直线中的任意两条直线都相交,若交点数最多为个,最少为个,则.
18. 已知条直线中的任意两条直线都相交,若交点数最多为个,最少为个,则.三、解答题
-
19. 计算:(1)、(2)、.20. 解方程:(1)、(2)、.21. 已知 .(1)、求 的值;(2)、求代数式 的值.22. 如图,点在直线上,平分 , ⊥.
 (1)、已知 , 求的大小;(2)、若 , 请通过计算判断是否平分.23. 某城市电费收取实施阶梯电价计费,具体方案如下:
(1)、已知 , 求的大小;(2)、若 , 请通过计算判断是否平分.23. 某城市电费收取实施阶梯电价计费,具体方案如下:用电时段
高峰期
低谷期
时段范围
第一天-
-第二天
电价
0.55元/度
0.30元/度
某日小强观察了一下自家的电能表,并分别记录了第一天早 , 晚和第二天早这三个时刻的读数分别是(单位:度).
(1)、求小强家这一天应付电费多少元?(2)、为节省开支,小强建议他爸不要在“高峰期”给电动车充电,改在“低谷期”充电,结果该天小强家应付电费为元,假定小强家每天电动车充电和其它用电的电量不变,求小强他爸的电动车充电用电多少度?24. 如图所示,点、在线段上,点、分别是、的中点. (1)、设 , 求线段的长;(2)、设 , , 用表示线段的长.25. 已知数轴上、两点对应的数分别为、.(1)、如果、两点的中点对应的数为 , 求的值;(2)、设点P以每秒钟个单位长度的速度从数轴上原点O出发,点、分别以每秒钟个单位长度和每秒钟个单位长度的速度出发,且三点同时向右运动,那么经过多少秒钟时,点P是、两点的中点?26. 我们把一个位整数(或位小数,为不小于2的自然数)按数位顺序移动各数位上的数,得到一个新的位整数叫做原数的“换位数”.比如:的“换位数”是;有两个“换位数”分别是;有三个“换位数”分别是.(1)、请写出的三个“换位数”.(2)、的“换位数”都是它本身,若表示以为单循环节的无限循环小数,其“换位数”也是它本身,则 , 请说明:;(3)、已知百位上的数为的一个三位数,其每个数位上的数互异且它们之和小于 , 如果这个三位数与它的两个“换位数”之和能被整除,求这个三位数.
(1)、设 , 求线段的长;(2)、设 , , 用表示线段的长.25. 已知数轴上、两点对应的数分别为、.(1)、如果、两点的中点对应的数为 , 求的值;(2)、设点P以每秒钟个单位长度的速度从数轴上原点O出发,点、分别以每秒钟个单位长度和每秒钟个单位长度的速度出发,且三点同时向右运动,那么经过多少秒钟时,点P是、两点的中点?26. 我们把一个位整数(或位小数,为不小于2的自然数)按数位顺序移动各数位上的数,得到一个新的位整数叫做原数的“换位数”.比如:的“换位数”是;有两个“换位数”分别是;有三个“换位数”分别是.(1)、请写出的三个“换位数”.(2)、的“换位数”都是它本身,若表示以为单循环节的无限循环小数,其“换位数”也是它本身,则 , 请说明:;(3)、已知百位上的数为的一个三位数,其每个数位上的数互异且它们之和小于 , 如果这个三位数与它的两个“换位数”之和能被整除,求这个三位数.