浙江省衢州市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
1. 下列各数中,比0大的数是( )A、1 B、0 C、﹣1 D、﹣22. 国家统计局发布一组数据,全国粮食品产量13390000000000斤,该数字用科学记数法表示为( )A、1.339×1014 B、1.339×1013 C、1.339×1012 D、1.339×10113. 下列运算正确的是( )A、a+a2=a3 B、4a2﹣2a2=2a2 C、3a﹣a=2 D、﹣2(a﹣2)=﹣2a﹣44. 如图,∠1和∠2是对顶角的图形是( )A、
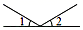 B、
B、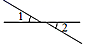 C、
C、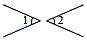 D、
D、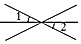 5. 若x=y+2,则下列式子一定成立的是( )A、x﹣y+2=0 B、x﹣2=﹣y C、2x=2y+2 D、6. 代数式的意义是( )A、x除以y加3 B、y加3除x C、y与3的和除以x D、x除以y与3的和所得的商7. 若x+y﹣3=0,则代数式﹣x﹣y+9的值是( )A、3 B、6 C、9 D、128. 大扫除期间,七(2)班已经安排了6人打扫教室,4人打扫包干区,为了尽快完成打扫任务,有14人主动要求去帮忙,使得打扫包干区的人数是打扫教室人数的2倍.假设去教室帮忙的同学有x人,根据题意可列出方程( )A、2(6+x)=4+(14﹣x) B、6+x=2[4+(14﹣x)] C、2[6+(14﹣x)]=4+x D、6+(14﹣x)=2(4+x)9. 杭衢高铁线上,要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘,需要印制不同的火车票( )A、20种 B、15种 C、10种 D、5种10. 按图示方法,搭1个正方形需要四根火柴,搭3个正方形需要10根火柴,搭6个正方形需要18根火柴棒,则能搭成符合规律图形的火柴棒的数目可以是( )
5. 若x=y+2,则下列式子一定成立的是( )A、x﹣y+2=0 B、x﹣2=﹣y C、2x=2y+2 D、6. 代数式的意义是( )A、x除以y加3 B、y加3除x C、y与3的和除以x D、x除以y与3的和所得的商7. 若x+y﹣3=0,则代数式﹣x﹣y+9的值是( )A、3 B、6 C、9 D、128. 大扫除期间,七(2)班已经安排了6人打扫教室,4人打扫包干区,为了尽快完成打扫任务,有14人主动要求去帮忙,使得打扫包干区的人数是打扫教室人数的2倍.假设去教室帮忙的同学有x人,根据题意可列出方程( )A、2(6+x)=4+(14﹣x) B、6+x=2[4+(14﹣x)] C、2[6+(14﹣x)]=4+x D、6+(14﹣x)=2(4+x)9. 杭衢高铁线上,要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘,需要印制不同的火车票( )A、20种 B、15种 C、10种 D、5种10. 按图示方法,搭1个正方形需要四根火柴,搭3个正方形需要10根火柴,搭6个正方形需要18根火柴棒,则能搭成符合规律图形的火柴棒的数目可以是( ) A、52根 B、66根 C、72根 D、88根
A、52根 B、66根 C、72根 D、88根二、填空题
-
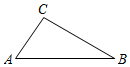
11. 单项式﹣5t的系数是.12. 计算:﹣1=.13. 如图,根据“两点之间线段最短”,可以判定AC+BCAB(填“>”“<”或“=”).
 14. 有一种“24点”游戏的规则:用4个整数进行有理数运算(可用括号和乘方)列出一个计算结果为24的算式,现有数2,﹣3,4,5,请列出“24点”的算式:(写出一个算式即可).15. 如表所示,已知a,b满足表格中的条件,则b的值是.
14. 有一种“24点”游戏的规则:用4个整数进行有理数运算(可用括号和乘方)列出一个计算结果为24的算式,现有数2,﹣3,4,5,请列出“24点”的算式:(写出一个算式即可).15. 如表所示,已知a,b满足表格中的条件,则b的值是.x
﹣1
ax
﹣1
ax2+b
4
16. 如图,一个瓶子的容积为1升,瓶内装着一些溶液,当瓶子正放时,瓶内溶液的高度为20cm,倒放时,空余部分的高度为5cm. (1)、瓶内溶液的体积为升;(2)、现把溶液全部倒在一个底面为60cm2的圆柱形杯子里,再把瓶子倒放,此时瓶内溶液的高度是圆柱形杯子内溶液高度的6倍.已知瓶子的高度是33cm,则倒入圆柱形杯子内的溶液体积为.
(1)、瓶内溶液的体积为升;(2)、现把溶液全部倒在一个底面为60cm2的圆柱形杯子里,再把瓶子倒放,此时瓶内溶液的高度是圆柱形杯子内溶液高度的6倍.已知瓶子的高度是33cm,则倒入圆柱形杯子内的溶液体积为.三、解答题
-
17. 计算:(1)、4+(﹣3)2×2.(2)、×6.18. 先化简,再求值;3(x2﹣3y)﹣(3x2+y﹣x),其中x=﹣2,y=.19.(1)、3x+3=2x﹣1;(2)、.20. 如图,已知线段AB.
 (1)、利用刻度尺画图:延长线段AB至C,使BC=AB,取线段AC的中点D.(2)、若CD=6,求线段BD的长.21. 如图1,依次连接2×2方格四条边的中点,得到一个阴影正方形,设每一方格的边长为1个单位,则这个阴影正方形的边长为.
(1)、利用刻度尺画图:延长线段AB至C,使BC=AB,取线段AC的中点D.(2)、若CD=6,求线段BD的长.21. 如图1,依次连接2×2方格四条边的中点,得到一个阴影正方形,设每一方格的边长为1个单位,则这个阴影正方形的边长为. (1)、图1中AB=AP=;点P表示的实数为.(2)、如图2,在4×4方格中阴影正方形的边长为a.
(1)、图1中AB=AP=;点P表示的实数为.(2)、如图2,在4×4方格中阴影正方形的边长为a.①写出边长a的值.
②请利用直尺和圆规在数轴上表示实数﹣a+1.
22. 如图,直线AB与直线CD相交于点O,OE⊥OF,且OA平分∠COE. (1)、若∠DOE=50°,求∠BOF的度数.(2)、设∠DOE=α,∠BOF=β,请探究α与β的数量关系(要求写出过程).23. (阅读理解)甲、乙两人分别从A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶,出发后经过0.4小时相遇,已知在相遇时乙比甲多行驶了14.4千米,相遇后经0.1小时乙到达A地.问甲、乙两人的速度分别是多少?
(1)、若∠DOE=50°,求∠BOF的度数.(2)、设∠DOE=α,∠BOF=β,请探究α与β的数量关系(要求写出过程).23. (阅读理解)甲、乙两人分别从A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶,出发后经过0.4小时相遇,已知在相遇时乙比甲多行驶了14.4千米,相遇后经0.1小时乙到达A地.问甲、乙两人的速度分别是多少?分析可以用示意图来分析本题中的数量关系.
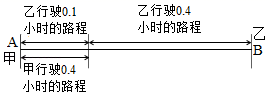
从图中可得如下的相等关系,
甲行驶0.4小时的路程=乙行驶0.1小时路程,
甲行驶0.4小时的路程+14.4=乙行驶0.4小时的路程.
根据这两个相等关系,可得到甲、乙速度的关系,设元列出方程.
(1)、(问题解决)请你列方程解答(阅读理解)中的问题.(2)、(能力提升)对于上题,若乙出发0.2小时后行驶速度减少10千米/小时,问甲出发后经多少小时两人相距2千米?