四川省成都市龙泉驿区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-12-28 类型:期末考试
一、单选题
-
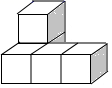
1. 如果“盈利5%”记作+5%,那么-3%表示( )A、亏损3% B、亏损8% C、盈利2% D、少赚3%2. 在-1,0, ,-4这四个数中,绝对值最大的数是( ).A、-1 B、 C、-4 D、03. 如图所示的几何体是由一些小正方体组成的,那么从左边看它的图形是( )
 A、
A、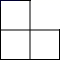 B、
B、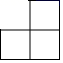 C、
C、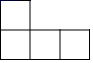 D、
D、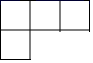 4. 作为2021年成都大运会主会场,东安湖体育中心项目将于今年4月底前全部完工,计划总投资约为50亿元.其中50亿用科学记数法表示为( ).A、5×108 B、0.5×1010 C、5×109 D、50×1085. 下列调查中,最适合采用全面调查(普查)的是( ).A、对我市中学生近视情况的调查 B、对我市市民国庆出游情况的调查 C、对全国人民掌握新冠防疫知识情况的调查 D、对我国自行研制的大型飞机C919各零部件质量情况的调查6. 下列计算正确的是( )A、5﹣=5 B、﹣3(a﹣b)=﹣3a+3b C、a+3b=4a D、2a+3b=5ab7. 若单项式2am+6b2n+1与a5b7的和仍是单项式,则m+n的值为( ).A、-4 B、4 C、-2 D、28. 若x=﹣3是关于x的方程2x+a=1的解,则a的值为( )A、﹣7 B、﹣5 C、7 D、59. 如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
4. 作为2021年成都大运会主会场,东安湖体育中心项目将于今年4月底前全部完工,计划总投资约为50亿元.其中50亿用科学记数法表示为( ).A、5×108 B、0.5×1010 C、5×109 D、50×1085. 下列调查中,最适合采用全面调查(普查)的是( ).A、对我市中学生近视情况的调查 B、对我市市民国庆出游情况的调查 C、对全国人民掌握新冠防疫知识情况的调查 D、对我国自行研制的大型飞机C919各零部件质量情况的调查6. 下列计算正确的是( )A、5﹣=5 B、﹣3(a﹣b)=﹣3a+3b C、a+3b=4a D、2a+3b=5ab7. 若单项式2am+6b2n+1与a5b7的和仍是单项式,则m+n的值为( ).A、-4 B、4 C、-2 D、28. 若x=﹣3是关于x的方程2x+a=1的解,则a的值为( )A、﹣7 B、﹣5 C、7 D、59. 如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( ) A、65° B、50° C、40° D、25°10. 有下列结论:①用一个平面去截正方体,截面可能是六边形;②正数和负数统称为有理数;③单项式 的系数是 ;④如果 ,那么 .其中正确结论的个数是( )A、1个 B、2个 C、3个 D、4个
A、65° B、50° C、40° D、25°10. 有下列结论:①用一个平面去截正方体,截面可能是六边形;②正数和负数统称为有理数;③单项式 的系数是 ;④如果 ,那么 .其中正确结论的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若 与-3互为相反数,则m的值为 .12. 若方程3xk﹣2=7是一元一次方程,那么k=.13. 已知m、n满足|2m+4|+(n﹣3)2=0,那么(m+n)2021的值为.14. 如图,已知线段AB=10cm,点N在线段AB上,NB=2cm,M是AB中点,那么线段MN的长为.
 15. 如图:点C为线段AB上的一点,M、N分别为AC、BC的中点,AB=40,则MN=.
15. 如图:点C为线段AB上的一点,M、N分别为AC、BC的中点,AB=40,则MN=. 16. 已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|c﹣b|+|a﹣c|=.
16. 已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|c﹣b|+|a﹣c|=. 17. 将两块直角三角尺的直角顶点重合为如图所示的位置,为等腰直角三角形,当绕点顺时针旋转度(),时,则.
17. 将两块直角三角尺的直角顶点重合为如图所示的位置,为等腰直角三角形,当绕点顺时针旋转度(),时,则. 18. 我们将圆形钟面的时针和分针看作是两条从圆心发出的射线,当时针和分针夹角180度时形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“平衡时刻”,如图,6点整就是一个平衡时刻,请问从0时到24时共有个平衡时刻.
18. 我们将圆形钟面的时针和分针看作是两条从圆心发出的射线,当时针和分针夹角180度时形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“平衡时刻”,如图,6点整就是一个平衡时刻,请问从0时到24时共有个平衡时刻. 19. 将长为2,宽为a的长方形纸片(1<a<2)如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若第3次操作后,剩下的长方形恰好是正方形,则a的值为.
19. 将长为2,宽为a的长方形纸片(1<a<2)如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若第3次操作后,剩下的长方形恰好是正方形,则a的值为. 20. 十八世纪伟大的数学家欧拉证明了简单多面体中顶点数(v),面数(f),棱数(e)之间存在一个有趣的数量关系:v+f﹣e=2,这就是著名的欧拉定理.而正多面体,是指多面体的各个面都是形状大小完全相同的的正多边形,虽然多面体的家族很庞大,可是正多面体的成员却仅有五种,它们是正四面体、正六面体、正八面体、正十二面体和正二十面体,那今天就让我们来了解下这几个立体图形中的“天之骄子”:
20. 十八世纪伟大的数学家欧拉证明了简单多面体中顶点数(v),面数(f),棱数(e)之间存在一个有趣的数量关系:v+f﹣e=2,这就是著名的欧拉定理.而正多面体,是指多面体的各个面都是形状大小完全相同的的正多边形,虽然多面体的家族很庞大,可是正多面体的成员却仅有五种,它们是正四面体、正六面体、正八面体、正十二面体和正二十面体,那今天就让我们来了解下这几个立体图形中的“天之骄子”: (1)、如图1,正四面体共有个顶点,条棱.(2)、如图2,正六面体共有个顶点,条棱.(3)、如图3是某个方向看到的正八面体的部分形状(虚线被隐藏),正八面体每个面都是正三角形,每个顶点处有四条棱,那么它共有个顶点,条棱.(4)、当我们没有正12面体的图形时,我们可以根据计算了解它的形状:我们设正12面体每个面都是正n(n≥3)边形,每个顶点处有m(m≥3)条棱,则共有12n÷2=6n条梭,有12n÷m=个顶点.欧拉定理得到方程:+12﹣6n=2,且m,n均为正整数,
(1)、如图1,正四面体共有个顶点,条棱.(2)、如图2,正六面体共有个顶点,条棱.(3)、如图3是某个方向看到的正八面体的部分形状(虚线被隐藏),正八面体每个面都是正三角形,每个顶点处有四条棱,那么它共有个顶点,条棱.(4)、当我们没有正12面体的图形时,我们可以根据计算了解它的形状:我们设正12面体每个面都是正n(n≥3)边形,每个顶点处有m(m≥3)条棱,则共有12n÷2=6n条梭,有12n÷m=个顶点.欧拉定理得到方程:+12﹣6n=2,且m,n均为正整数,去掉分母后:12n+12m﹣6nm=2m,
将n看作常数移项:12m﹣6nm﹣2m=﹣12n,
合并同类项:(10﹣6n)m=﹣12n,
化系数为1:m= ,
变形: ,
= ,
= ,
= ,
=.
分析:m(m≥3),n(n≥3)均为正整数,所以是正整数,所以n=5,m=3,即6n=30,.
因此正12面体每个面都是正五边形,共有30条棱,20个顶点.
请依据上面的方法或者根据自己的思考得出:正20面体共有条棱;个顶点.
三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 解方程:(1)、(2)、23. 解下列不等式(组),并把解集在数轴上表示出来(1)、;
 (2)、.
(2)、. 24. 先化简,再求值:2(xy+5x2y)﹣3(3xy2﹣xy)﹣xy2 , 其中x,y满足x=﹣1,y=﹣.25. 新学期,龙泉某中学开设了“家校心理疏导”课程.为了解学生的前置情况,从七年级学生中随机抽取了部分学生进行一次综合测试,测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D为不及格,将测试结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题:
24. 先化简,再求值:2(xy+5x2y)﹣3(3xy2﹣xy)﹣xy2 , 其中x,y满足x=﹣1,y=﹣.25. 新学期,龙泉某中学开设了“家校心理疏导”课程.为了解学生的前置情况,从七年级学生中随机抽取了部分学生进行一次综合测试,测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D为不及格,将测试结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题: (1)、本次抽样测试的人数是名;(2)、扇形统计图中表示A级的扇形圆心角α的度数是 ▲ , 并把条形统计图补充完整;(3)、该校七年级共有学生400名,如果全部参加这次测试,估计不及格的人数为多少?26. 列方程解应用题:一件衬衫先按进价加价60元标价,再以8折出售,仍可获利24元,这件衬衫的进价是多少钱?
(1)、本次抽样测试的人数是名;(2)、扇形统计图中表示A级的扇形圆心角α的度数是 ▲ , 并把条形统计图补充完整;(3)、该校七年级共有学生400名,如果全部参加这次测试,估计不及格的人数为多少?26. 列方程解应用题:一件衬衫先按进价加价60元标价,再以8折出售,仍可获利24元,这件衬衫的进价是多少钱?审题:A: ▲ .
B:
进价
标价
折数
售价
利润
C:设 ▲ .
27. 列方程解应用题:某工有中、乙两车间各生产不同型号的产品,原计划乙车间人数比甲车间少100人,产品上市后,甲车间的产品成为爆款,于是又从乙车间调50人支援甲车间,这时甲车间的人数是乙车间剩余人数的3倍,求原来甲乙车间各有多少人?28. 如图,已知数轴上两点A,B表示的数分别为﹣3,9,用符号“AB”来表示点A和点B之间的距离. (1)、若在数轴上存在一点C,使AC=3BC,求点C表示的数;(2)、在(1)的条件下,点C位于A,B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动,设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.(3)、在(1)的条件下,点C位于A,B两点之间.点A以1个单位/秒的速度沿着数轴的负方向运动,2秒后点B以2个单位/秒的速度也沿着数轴的负方向运动.点C以20单位/秒的速度与点A同时同向出发,当遇到A后,立即返回向B点运动;遇到B点后立即返回向A点运动:如此往返,直到B追上A时,C立即停止运动,那么点C从开始到停止运动,运动的路程是多少单位长度.
(1)、若在数轴上存在一点C,使AC=3BC,求点C表示的数;(2)、在(1)的条件下,点C位于A,B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动,设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.(3)、在(1)的条件下,点C位于A,B两点之间.点A以1个单位/秒的速度沿着数轴的负方向运动,2秒后点B以2个单位/秒的速度也沿着数轴的负方向运动.点C以20单位/秒的速度与点A同时同向出发,当遇到A后,立即返回向B点运动;遇到B点后立即返回向A点运动:如此往返,直到B追上A时,C立即停止运动,那么点C从开始到停止运动,运动的路程是多少单位长度.