湘教版初中数学九年级下册第二章圆 单元测试
试卷更新日期：2021-12-27 类型：单元试卷
一、单选题
-
1. Rt△ABC中，∠C=90°，AC=2，BC=4，如果以点为圆心，AC为半径作⊙A，那么斜边AB的中点D与⊙A的位置关系是（ ）．A、点D在⊙A外 B、点D在⊙A上 C、点D在⊙A内 D、无法确定2. 如图，AB是⊙O的直径，CD是⊙O的弦，如果∠ACD=36°，那么∠BAD等于（ ）．
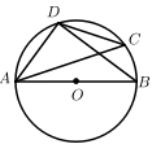A、36° B、44° C、54° D、56°3. 如图，PA、PB分别切⊙O于A，B，∠APB=60°，⊙O半径为2，则PB的长为（ ）．
A、3 B、4 C、 D、4. 如图，△ABC是一张周长为18cm的三角形纸片，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，若剪下的三角形的周长为8cm，则BC为（ ）
A、8cm B、5cm C、6.5cm D、无法确定5. 如图所示，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA，OB在O点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE＝8个单位，OF＝6个单位，则圆的直径为（ ）
A、12个单位 B、10个单位 C、1个单位 D、15个单位6. 下列图形中的角是圆周角的是（ ）A、
B、
C、
D、
7. 如图，从圆外一点P引圆的两条切线PA，PB，A，B为切点，C为PB上的一点，连接CO交⊙O于点D，若 ， ， ，则⊙O的半径长是（ ）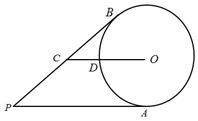
A、 B、 C、4 D、38. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于（ ）
A、20° B、30° C、40° D、50°9. 如图，点A、B、C是⊙O上的三个点，若∠AOB＝82°，则∠C的度数为（ ）
A、82° B、38° C、24° D、41°10. 已知 是半径为6的圆的一条弦，则 的长不可能是（ ）A、8 B、10 C、12 D、14二、填空题
-
11. 若扇形的圆心角为90°，半径为4，则该扇形的弧长为 ．12. 如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为 ．
13. 在半径为2的圆O中有一条弦AB=2 ，则弦AB所对的圆周角度数为14. 如图，若以AB为边长作⊙O的内接正多边形，则这个多边形是正边形．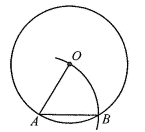
15. 如图，点P为⊙O外一点，PA，PB分别与⊙O相切于点A，B，∠APB＝90°.若⊙O的半径为2，则图中阴影部分的面积为（结果保留π）.
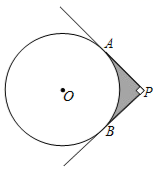16. 如图，在平面直角坐标系xOy中，点A，B，C的坐标分别是（0，4），（4，0），（8，0），⊙M是△ABC的外接圆，则点M的坐标为.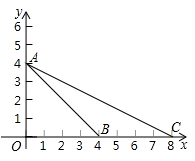
三、解答题
-
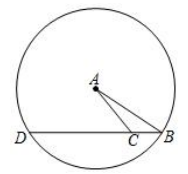
17. 如图，在△ABC中AB＝5，AC＝4，BC＝2，以A为圆心，AB为半径作⊙A，延长BC交⊙A于点D，试求CD的长．
18. 如图所示，一座圆弧形拱桥的跨度AB长为40米，桥离水面最大距离CD为10米，若有一条水面上宽度为30米，宽度为6米的船能否通过这座桥？请说明理由．
19. 如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切于点C时，另一边与圆两个交点A和B的读数恰好为“2”和“8”（单位：cm）求该圆的半径．
20. 如图， 和 是⊙ 的两条切线，A，B是切点．C是 上任意一点，过点C画⊙ 的切线，分别交 和 于D，E两点，已知 ，求 的周长．
四、综合题
-
21. 如图，△ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
(1)、求证：∠ACD= ∠B；(2)、若BC＝6，AC＝8，求AD和CD的长．22. 如图，在边长为1的正方形组成的网格中建立直角坐标系， 的顶点均在格点上，点O为原点，点A、B的坐标分别是 、 ．
(1)、将 向下平移2个单位后得到 ，则点 的坐标为；(2)、将 绕点O逆时针旋转 后得到 ，请在图中作出 ，并求出这时点 的坐标为 ▲ ；(3)、在（2）中的旋转过程中，求线段OB扫过的图形的面积．23. 如图，PA为⊙O的切线，A为切点，过点A作AB⊥OP，垂足为点C，交⊙O于点B，延长BO与PA的延长线交于点D．
(1)、求证：PB为⊙O的切线；(2)、若OB=3，OD=5，求OP的长．24. 在 中， ， ， 是 边上的点，⊙O与 相切，切点为 ， 与⊙O相交于点 ，且 ．
(1)、求证： 是⊙O的切线；(2)、如果 为 弧上的一个动点（不与 、 重合），过点 作⊙O的切线分别与边 、 相交于 、 ，连接 、 ，有两个结论：①四边形 的周长不变，② 的度数不变．已知这两个结论只有一个符合题意，找出正确的结论并证明；(3)、探究：在（2）的条件下，设 ， ，试问 与 之间满足怎样的函数关系，写出你的探究过程并确定变量 的取值范围，并说明当 时 点的位置．