湘教版初中数学九年级下册第一章二次函数单元测试

试卷更新日期：2021-12-27 类型：单元试卷

进入出卷网下载

一、单选题

1. 抛物线y＝2x²﹣3的顶点坐标是（）

A、（3，0） B、（﹣3，0） C、（0，3） D、（0，﹣3）

查看试题解析
2. 在下列抛物线中，其顶点是(－2，4)的是（）．

A、y＝(x+2)²﹣4 B、y＝(x－2)²+4 C、y＝(x+2)²+4 D、y＝(x－2)²﹣4

查看试题解析
3. 我们把“将抛物线向右平移2个单位或．向上平移1个单位”这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后得到的一条抛物线是y=x²+1，则原抛物线的表达式不可能是（）．

A、y=x²－1 B、y=x²+6x+5 C、y=x²+4x+4 D、y=x²+8x+17

查看试题解析
4. 已知二次函数y＝x²－bx+c的图象经过A（1，n），B（3，n），且与x轴只有一个交点，则n的值为（）．

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
5. 若二次函数y＝x²﹣6x+k的图象经过A（﹣1，y₁），B（1，y₂），C（3+ $\sqrt{3}$ ，y₃）三点，则y₁ ， y₂ ， y₃关系正确的是（）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₂＞y₁＞y₃ D、y₃＞y₁＞y₂

查看试题解析
6. 如图是抛物线y=ax²+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），有下列结论：①2a+b=0，②abc＞0；③方程ax²+bx+c=3有两个相等的实数根，④当y＜0时，﹣2＜x＜4，其中正确的是（）

A、②③ B、①③ C、①③④ D、①②③④

查看试题解析
7. 如图，已知二次函数 $y_{1} = {(x + 1)}^{2} - 3$ 向右平移2个单位得到抛物线 $y_{2}$ 的图象，则阴影部分的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 求二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，其对称轴为直线 $x = - 1$ ，与 $x$ 轴的交点为 $(x_{1} ， 0)$ 、 $(x_{2} ， 0)$ ，其中 $0 < x_{1} < 1$ ，有下列结论：① $a b c > 0$ ；② $- 3 < x_{2} < - 2$ ；③ $4 a - 2 b + c < - 1$ ；④ $a - b > a m^{2} + b m (m \neq - 1)$ ；⑤ $a > \frac{1}{3}$ ；其中，正确的结论有（）

A、5 B、4 C、3 D、2

查看试题解析
9. 下表是满足二次函数 $y = a x^{2} + b x + c$ 的五组数据， $x = m$ 是方程 $0 = a x^{2} + b x + c$ 的一个解，则下列选项中正确的是（）

x

1.6

1.8

2.0

2.2

2.4

y

-0.80

-0.54

-0.20

0.22

0.2

A、 $1.6 < m < 1.8$ B、 $1.8 < m < 2.0$ C、 $2.0 < m < 2.2$ D、 $2.2 < m < 2.4$

查看试题解析
10. 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米．当喷射出的水流距离喷水头20米时．达到最大高度11米，现将喷灌架置于坡度为1：10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB ，因为刚刚被喷洒了农药，近期不能被喷灌．下列说法正确的是（　　）

A、水流运行轨迹满足函数y＝﹣ $\frac{1}{40}$ x²﹣x+1 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米，可以避开对这棵石榴树的喷灌

查看试题解析

二、填空题

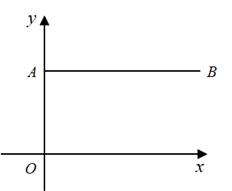
11. 将抛物线y=x²+1沿x轴向下翻折，则得到的新抛物线的解析式为．

查看试题解析
12. 如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（6，3）．若抛物线y＝mx²＋2mx＋m＋3（m为常数，m≠0）向右平移a（a＞0）个单位长度，平移后的抛物线的顶点在线段AB上，则a的取值范围为．

查看试题解析
13. 设二次函数y＝x²+2x－3的图象为C₁ ，关于x的一次函数y＝kx+3k的图象为C₂.

(1)、C₁和C₂恰好都经过定点P，则点P的坐标为；

(2)、若C₁和C₂有两个不同的交点，设其横坐标分别为x₁和x₂ ，且x₁＜x₂＜1，则k的取值范围为．

查看试题解析
14. 二次函数y=2x²+(m-1)x-3的顶点在y轴上，则m= ．

查看试题解析
15. 二次函数y＝x²﹣4x+1的最小值是．

查看试题解析
16. 如图，把抛物线 $y = x^{2}$ 沿直线 $y = x$ 平移 $\sqrt{2}$ 个单位后，其顶点在直线上的A处，则平移后抛物线的表达式是．

查看试题解析

三、作图题

17. 二次函数y＝ax²+bx+c（a≠0）的自变量x与对应的函数y的值（部分）如表所示：

x	…	﹣3	﹣2	﹣1	0	1	2	…
y	…	m	﹣2	﹣3	﹣2	1	6	…

解答下列问题：

(1)、表格中m的值等于；

(2)、求这个二次函数的解析式；

(3)、在直角坐标系中，画出这个函数的图象．

查看试题解析

18. 如图，在平面直角坐标系中，矩形OABC的顶点C，A分别在x轴，y轴上，经过A，C两点的抛物线交x轴于另一点D，连接AC．请仅用无刻度的直尺完成以下作图．（保留作图痕迹）

(1)、在图1中的抛物线上找出点E，使 $D E = A C$ ．

(2)、在图2中的抛物线上作出该抛物线的顶点F．

查看试题解析

四、解答题

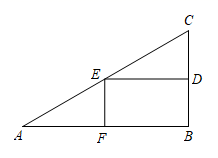
19. 已知抛物线的顶点坐标是（1，﹣3），与y轴的交点是（0，﹣2），求这个二次函数的解析式.

查看试题解析
20. 现有一块直角三角形的材料， $A B = 80$ cm， $B C = 60$ cm，用它截下一个矩形，如图是截法示意图，求这种截法下矩形的最大面积是多少？

查看试题解析
21. 如图的一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线解析式是 $t = - 2 x + 80$ ，求选取点B为坐标原点时的抛物线解析式．

查看试题解析

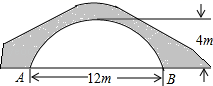
五、综合题

22. 如图，已知二次函数y＝﹣x²＋bx＋c的图象经过点A（﹣2，0），B（6，0），与y轴交于点C．

(1)、求抛物线的解析式；

(2)、抛物线的对称轴上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P的坐标，若不存在，请说明理由．

查看试题解析
23. 若抛物线的顶点坐标是（﹣4，3），且过点（﹣5，1）．

(1)、求此抛物线的函数关系式．

(2)、直接写出当﹣6＜x＜﹣1时，y的取值范围．

查看试题解析
24. 在平面直角坐标系中，函数y＝﹣x²＋2mx＋2m＋1的图像记为G，抛物线G的自变量x的取值范围为x≤2m，m为常数．

(1)、当点（0，3）在图象G上时，求m的值．

(2)、抛物线G上有一点B到y轴的最小距离为2，求点B的坐标．

(3)、在平面直角坐标系中，点P的坐标为（m，﹣m²＋m＋3）．
①当图象G的最高点的纵坐标与点P的纵坐标之差为1时，求m的值．

②将点P向左平移4个单位长度得到点Q，连结PQ．以PQ为边向上方作矩形PQMN，使PN＝2，当图象G在矩形PQMN内的部分所对应的函数值y随x的增大而增大时，直接写出m的取值范围．

查看试题解析
25. 已知，平面直角坐标系中，抛物线 $= a x^{2} + k$ 交y轴于点A，交x轴于点B、C， $△ A B C$ 为等边三角形， $B C = 10$ ．

(1)、如图1，求抛物线解析式．

(2)、如图2，P为AC上方抛物线上一点，过P作 $P D ∥ A O$ 交AC于D，设点P的横坐标为t，PD的长度为d，求d与t的函数关系式；

(3)、如图3，在（2）的条件下，在x轴上点B左侧取一点E，使得点E在AD的垂直平分线上，连接ED，若 $△ C D E$ 的周长为36，求d的值．

查看试题解析

x	1.6	1.8	2.0	2.2	2.4
y	-0.80	-0.54	-0.20	0.22	0.2

湘教版初中数学九年级下册第一章二次函数 单元测试

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

湘教版初中数学九年级下册第一章二次函数单元测试