河南省重点高中2021-2022学年高二上学期理数阶段性调研联考试卷
试卷更新日期:2021-12-24 类型:月考试卷
一、单选题
-
1. 经过点且在轴上的截距为的直线方程是( )A、 B、 C、 D、2. 两条平行直线 与 间的距离等于( )A、 B、 C、 D、3. 已知方程 表示圆,则实数k的取值范围是( )A、 B、 C、 D、 或4. 若直线 平分圆 ,则实数 的值为( )A、 B、 C、 D、 或5. 已知双曲线C: ( , )的实轴长为4,左焦点F到C的一条渐近线的距离为3,则C的方程为( )A、 B、 C、 D、6. 设 是椭圆 的两个焦点,若 上存在点 满足 ,则 的取值范围是( )A、 B、 C、 D、7. 与圆及圆都外切的圆的圆心在( )A、一个圆上 B、一个椭圆上 C、双曲线的一支上 D、抛物线上8. 若过点的直线与抛物线有且只有一个交点,则这样的直线共有( )条数.A、0 B、1 C、2 D、39. 直角坐标系xOy中,双曲线 的左焦点为F,A(1,4),P是右支上的动点,则|PF|+|PA|的最小值是( )A、8 B、9 C、10 D、1210. 已知过抛物线 的焦点 的直线交抛物线于 两点,以 为直径的圆过点 ,则 的值为( )A、 B、 C、 D、1011. 已知椭圆的左、右焦点分别为F、E,直线x=m(﹣1<m<1)与椭圆相交于点A、B,则( )A、当m=0时,△FAB的面积为1 B、不存在m使△FAB为直角三角形 C、存在m使四边形FBEA面积最大 D、存在m,使△FAB的周长最大12. 在直角坐标平面上,点的坐标满足方程 , 点的坐标满足方程则的取值范围是( )A、 B、 C、 D、
二、填空题
-
13. 已知直线经过点P , 且在两坐标轴上的截距相等,则直线的方程为 .14. 过点(1,2)总可作两条直线与圆相切,则实数的取值范围是.15. 已知直三棱柱 的各顶点都在同一球面上,若 , ,则该球的表面积等于 .16. 将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
⑴AC⊥BD;
⑵△ACD是等边三角形;
⑶AB与平面BCD所成的角为60°;
⑷AB与CD所成的角为60°.
则正确结论的序号为
三、解答题
-
17. 平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以100元罚款,记\text{3}分的行政处罚.如表是本市一主干路段监控设备所抓拍的5个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份
1
2
3
4
5
违章驾驶员人数
120
105
100
90
85.
(Ⅰ)请利用所给数据求违章人数与月份之间的回归直线方程;
(Ⅱ)预测该路段月份的不“礼让斑马线”违章驾驶员人数.
参考公式: , .
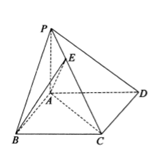
18. 如图,在正三棱柱 中, 为 的中点. (1)、证明: 平面 ;(2)、证明: 平面 ;(3)、若 ,求直线 与平面 所成角的正弦值.19. 某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组 , , …, , 其部分频率分布直方图如图所示.观察图形,回答下列问题.
(1)、证明: 平面 ;(2)、证明: 平面 ;(3)、若 ,求直线 与平面 所成角的正弦值.19. 某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组 , , …, , 其部分频率分布直方图如图所示.观察图形,回答下列问题. (1)、求成绩在的频率,并补全这个频率分布直方图:(2)、估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)(3)、从成绩在和的学生中选两人,求他们在同一分数段的概率.
(1)、求成绩在的频率,并补全这个频率分布直方图:(2)、估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)(3)、从成绩在和的学生中选两人,求他们在同一分数段的概率.