浙江省衢州市衢江区2020-2021学年八年级上学期数学期末考试试卷_
试卷更新日期：2021-12-24 类型：期末考试
一、单选题
-
1. 下列图标中轴对称图形的是（ ）A、
B、
C、
D、
2. 在平面直角坐标系中，点P（3，﹣2）在第（ ）象限A、一 B、二 C、三 D、四3. 如果a＜b，那么下列各式中正确的是（ ）A、a﹣1＞b﹣1 B、 C、﹣a＜﹣b D、﹣a+5＜﹣b+54. 不等式组 的解在数轴上表示为（ ）A、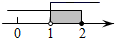
B、
C、
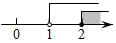D、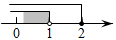
5. 直角三角形两直角边长分别为3cm和5cm，则这个直角三角形的周长是（ ）A、12cm B、（8 ）cm C、12cm或（8 ）cm D、11cm或13cm6. 一幅三角板，如图所示叠放在一起，则图中∠ 的度数是（ ）
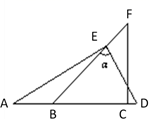A、75° B、60° C、65° D、55°7. 一次函数y＝kx＋b(k≠0)的图象如图所示，当y＞0时，x的取值范围是（ ）
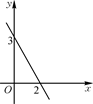A、x＜0 B、x＞0 C、x＜2 D、x＞28. 如图，为了估计一池塘岸边两点A，B之间的距离，小颖同学在池塘一侧选取了一点P，测得PA＝100m，PB＝90m，那么点A与点B之间的距离可能是（ ）
A、10m B、120m C、190m D、220m9. 如图， 顶角为120°， ， ，现将 折叠，使点 与点 重合，折痕为 ，则 的长为（ ）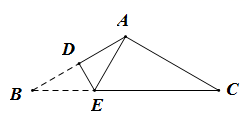
A、1 B、2 C、 D、10. 在平面直角坐标系中，O为坐标原点，已知点A，B的坐标分别是（2，0），（4，2），若在x轴下方有一点P，使以O，A，P为顶点的三角形与△OAB全等，则满足条件的P点的坐标是（ ）A、（4，﹣2） B、（﹣4，﹣2） C、（4，﹣2）或（﹣2，﹣2） D、（4，﹣2）或（﹣4，﹣2）二、填空题
-
11. 一元一次不等式x﹣5＜0的解是 .12. 命题“线段垂直平分线上的点到线段两端的距离相等”是 .（填“真命题”或“假命题”）13. 等腰三角形的一个底角为 ，则它的顶角的度数为 ．
14. 点A的坐标为（﹣1，2），点A到x轴的距离是 .15. 如图，在等边△ABC的AC，BC边上各取一点P，Q使AP＝CQ，AQ，BP相交于点O，则∠BOQ＝度.
16. 甲、乙两人相约周末登全旺饭甄山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
(1)、b＝米；(2)、若乙提速后，乙登山上升速度是甲登山上升速度的3倍，则甲、乙两人相遇后，再经过 分钟，他们俩距离地面的高度差为70米.三、解答题
-
17. 解一元一次不等式组 .18. 如图，AF＝DC ， ∠BCA＝∠EFD ， BC＝EF ， 求证：△ABC≌△DEF ．
19. 已知y是关于x的一次函数，且当x＝1时，y＝4；当x＝﹣1时，y＝8.(1)、求该函数表达式；(2)、在平面直角坐标系中，O为坐标原点，设该一次函数与x轴、y轴交点分别是A、B两点，求△ABO的面积.20. 如图，在△ABC中，点D是BC边上一点，连接AD，若AB＝10，AC＝17，BD＝6，AD＝8.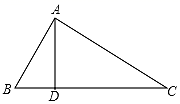
(1)、求∠ADB的度数；(2)、求BC的长.21. 如图(1)，矩形纸片ABCD，把它沿对角线BD向上折叠，
(1)、在图(2)中用实线画出折叠后得到的图形(要求尺规作图，保留作图痕迹，不写作法)(2)、折叠后重合部分是什么图形？说明理由.22. 我国传统的计重工具——秤的应用，方便了人们的生活，如图1，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量.称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤）.如表中为若干次称重时所记录的一些数据.x（厘米）
1
2
4
7
y（斤）
0.75
1.00
1.50
2.25
(1)、在图2中将表x，y的数据通过描点的方法表示，观察判断x，y的函数关系，并求秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少斤？(2)、已知秤砣到秤纽的最大水平距离为50厘米，这杆秤的可称物重范围是多少斤？23. 近期疫情防控形势严峻.妈妈让小明到惠民药店购买口罩.某种包装的口罩标价每袋10元，请认真阅读老板与小明的对话：
(1)、结合两人的对话内容，小明原计划购买几袋口罩？(2)、小明正准备结账时，妈妈来电话说还需要购买消毒液和洗手液共5瓶，三种物品购买总价不超过200元，现已知消毒液标价每瓶20元，洗手液标价每瓶35元，经过沟通，三种物品老板都给予8折优惠，那么小明最多可购买洗手液多少瓶？24. 定义：到三角形两个顶点距离相等的点叫做此三角形的准心.举例：如图1，若PA＝PB，则点P为△ABC的准心.
(1)、判断：如图2，△ABC中，AB＝AC，AD平分∠BAC，点P在AD上，则点P△ABC的准心（填“是”或“不是”）(2)、应用：如图3，CD为正△ABC的高，准心P在高CD上，且PD AB，求∠APB的度数；(3)、探究：已知△ABC为直角三角形，斜边BC＝5，AB＝3，准心P在AC边上，试探究PA的长.