浙江省丽水市莲都区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各点属于第一象限的是（）

A、（1，﹣2） B、（1，2） C、（﹣1，﹣2） D、（﹣1，2）

查看试题解析
2. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若2x＜2y，则下列不等式中一定成立的是（）

A、x＋y＜0 B、x＋y＞0 C、x﹣y＜0 D、x﹣y＞0

查看试题解析
4. 在平面直角坐标系中，把点A（﹣1，﹣3）先向右平移2个单位，再向上平移3个单位，所得点的坐标是（）

A、（﹣3，0） B、（1，0） C、（﹣3，﹣6） D、（1，﹣6）

查看试题解析
5. 如图，已知AB=DC ，下列条件中，不能使△ABC≌△DCB的是（）

A、AC=DB B、∠A=∠D=90° C、∠ABC=∠DCB D、∠ACB=∠DBC

查看试题解析
6. 一次函数 $y = - 3 x + 1$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 不等式组 ${\begin{matrix} 2 x \geq - 2 \\ x + 3 < 4 \end{matrix}$ 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
8. 如图，在△ABC中，用圆规在BA，BC上分别截取BD，BE，使BD=BE，分别以D，E为圆心、大于 $\frac{1}{2}$ DE的长为半径画弧，两弧在∠ABC内交于点F，连接BF并延长交AC于点G.若AB=3，BC=5，S_△ABC=32，则△BCG的面积是（）

A、20 B、 $\frac{96}{5}$ C、 $\frac{64}{5}$ D、12

查看试题解析
9. 若一次函数y=（4﹣3m）x﹣2的图象经过点A（x₁ ， y₁）和点B（x₂ ， y₂），当x₁＜x₂时，y₁＞y₂则m的取值范围是（）

A、m＜ $\frac{3}{4}$ B、m＞ $\frac{3}{4}$ C、m＜ $\frac{4}{3}$ D、m＞ $\frac{4}{3}$

查看试题解析
10. △ABC中，∠A=90°，∠B=60°，AB=2，若点D是BC边上的动点，则2AD+DC的最小值为（）

A、4 B、 $\sqrt{3}$ ＋3 C、6 D、2 $\sqrt{3}$ ＋3

查看试题解析

二、填空题

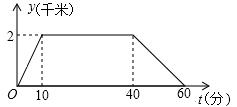
11. “x的2倍与3的差小于5”用不等式表示为：.

查看试题解析
12. △ABC中，AB＝3，AC＝4，则BC的长可能是（写出一个即可）.

查看试题解析
13. 在平面直角坐标系中，点P（－3，4）到x轴的距离为.

查看试题解析
14. 星期天，小明上午8：00从家里出发，骑车到图书馆去借书，再骑车回到家.他离家的距离y（千米）与时间t（分钟）的关系如图所示，则上午8：45小明离家的距离是千米.

查看试题解析
15. 如图，等边三角形ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF＝95°，则∠EGC的度数为.

查看试题解析
16. 如图，在平面直角坐标系中，直线y＝kx＋4经过点A（3，0），与y轴交于点B.

(1)、k的值为；

(2)、y轴上有点M（0， $\frac{12}{5}$ ），线段AB上存在两点P，Q，使得以O，P，Q为顶点的三角形与 $△$ OMP全等，则符合条件的点P的坐标为.

查看试题解析

三、解答题

17. 解不等式5x﹣2＞3（x﹣2）.

查看试题解析
18. 已知：如图，∠1＝∠2，∠B＝∠AED ， BC＝ED ．
求证：AB＝AE ．

查看试题解析
19. 已知：△ABC的三个顶点坐标分别是A（﹣2，0）.B（1，3），C（3，﹣2）.

(1)、在平面直角坐标系中画出△ABC；

(2)、判断△ABC的形状，并说明理由.

查看试题解析
20. 在国内投寄平信应付邮资如表：

信件质量x（克）

0＜x≤20

20＜x≤40

40＜x≤60

邮资y（元/封）

1.20

2.40

3.60

(1)、根据函数的定义，y是关于x的函数吗？

(2)、结合表格解答：
①求出当x=48时的函数值，并说明实际意义.

②当寄一封信件的邮资是2.40元时，信件的质量大约是多少克？

查看试题解析
21. 如图，△ABC中，∠ABC=90°，BA=BC，点F为CB延长线上一点，点E在AB上，且AF=CE.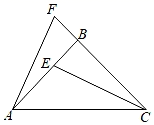

(1)、求证：△ABF≌△CBE；

(2)、若∠ACE=27°，求∠CAF的度数.

查看试题解析
22. 某水果经销商需购进甲，乙两种水果进行销售.甲种水果每千克的价格为a元，如果一次购买超过40千克，超过部分的价格打八折，乙种水果的价格为25元/千克.设经销商购进甲种水果x千克，付款y元，y与x之间的函数关系如图所示.

(1)、求a的值，并写出当x＞40时，y与x之间的函数关系式；

(2)、若经销商计划一次性购进甲，乙两种水果共80千克，且甲种水果不少于30千克，但又不超过50千克.如何分配甲，乙两种水果的购进量，才能使经销商付款总金额w（元）最少？

查看试题解析
23. 如果三角形有一边上的中线长恰好等于这边的长，则称这个三角形为“美好三角形”.

(1)、等边△ABC的边长为2，△ABC是“美好三角形”吗？请说明理由；

(2)、已知Rt△ABC是“美好三角形”，∠C＝90°，AC＝2 $\sqrt{3}$ ，求BC的长.

查看试题解析
24. 如图，在平面直角坐标系中，直线l₁：y＝x＋4交y轴于点A，直线l₂：y＝﹣x与l₁交于点B.

(1)、求点B的坐标；

(2)、在y轴左侧，有一条平行于y轴的动直线，分别与l₁ ， l₂交于点M、N，且点M在点N的上方.
①当MN＝2时，求△BMN的面积；

②点Q为y轴上一动点若△MNQ是以NQ为直角边的直角三角形，且两直角边长之比为3∶4，求出满足条件所有点Q的坐标.

查看试题解析

信件质量x（克）	0＜x≤20	20＜x≤40	40＜x≤60
邮资y（元/封）	1.20	2.40	3.60