四川省眉山市青神县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-12-24 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、±2 B、2 C、﹣2 D、±2. 要使二次根式 有意义,字母 必须满足的条件是( )A、 B、 C、 D、3. 点 关于 轴对称的点 的坐标是( )A、 B、 C、 D、4. 点 离原点的距离是( )A、4 B、7 C、3 D、55. 如图,等边△ABC的边长为2,AD是BC边上的高,则高AD的长为( )
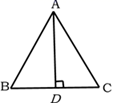 A、 B、 C、 D、6. 下列命题是真命题的是( )A、有两边及一角对应相等的两个三角形全等 B、角不是轴对称图形 C、底角相等的两个等腰三角形全等 D、若 ,则7. 如图,直线 ,将一块含 角( )的直角三角尺按图中方式放置,其中 和 两点分别落在直线 和 上.若 ,则 的度数为( )
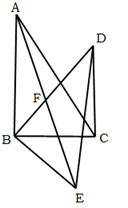
A、 B、 C、 D、6. 下列命题是真命题的是( )A、有两边及一角对应相等的两个三角形全等 B、角不是轴对称图形 C、底角相等的两个等腰三角形全等 D、若 ,则7. 如图,直线 ,将一块含 角( )的直角三角尺按图中方式放置,其中 和 两点分别落在直线 和 上.若 ,则 的度数为( )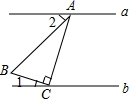 A、 B、 C、 D、8. 函数 满足 ,则函数图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 面试时,某应聘者的学历、经验和工作态度的得分分别是72分、86分、60分,若依次按照1:3:2的比例确定成绩,则该应聘者的最终成绩是( )A、75 B、72 C、70 D、6510. 若关于x、y的方程组 的解互为相反数,则m的值为( )A、-7 B、10 C、-10 D、-1211. 已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
A、 B、 C、 D、8. 函数 满足 ,则函数图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 面试时,某应聘者的学历、经验和工作态度的得分分别是72分、86分、60分,若依次按照1:3:2的比例确定成绩,则该应聘者的最终成绩是( )A、75 B、72 C、70 D、6510. 若关于x、y的方程组 的解互为相反数,则m的值为( )A、-7 B、10 C、-10 D、-1211. 已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是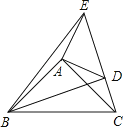 A、1 B、2 C、3 D、412. 一列数 , , ,…,具有下面的规律, , ,若 ,则 的值是( )A、1 B、3 C、6 D、13
A、1 B、2 C、3 D、412. 一列数 , , ,…,具有下面的规律, , ,若 ,则 的值是( )A、1 B、3 C、6 D、13二、填空题
-
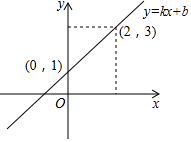
13. , .14. 方程组 的解是 .15. 若一组数据1,2,3,x,0,3,2的众数是3,则这组数据的中位数是.16. 将命题“对顶角相等”改为“如果…那么…”的形式为:.17. 一次函数 (k、b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于 的方程 的解为 .
 18. 如图,正方形ABCD,边长为4,点E是CD边的中点,F在边BC上,沿AF对折△ABF,点B落在AE上的G点处,则 .
18. 如图,正方形ABCD,边长为4,点E是CD边的中点,F在边BC上,沿AF对折△ABF,点B落在AE上的G点处,则 .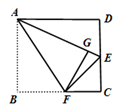 19. 已知CD是△ABC的边AB上的高,若CD= ,AD=1,AB=2AC,则BC的长为 .20. 观察下列等式:30=1,31=3,32=9,33=27,34=81,35=243,…,根据其中规律可得30+31+32+…+32018的结果的个位数字是 .
19. 已知CD是△ABC的边AB上的高,若CD= ,AD=1,AB=2AC,则BC的长为 .20. 观察下列等式:30=1,31=3,32=9,33=27,34=81,35=243,…,根据其中规律可得30+31+32+…+32018的结果的个位数字是 .
三、解答题
-
21.22. 解下列方程组23. 列方程组解应用题:
中国新型量子计算机“九章”,在实现“高斯玻色取样”任务的快速求解时,“九章”只用了1分钟,现在最先进的超级计算机要算上一亿年.而《九章算术》是中国古代第一部数学专著,也是世界上最早的印刷本数学书.书中有如下问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?大意是:有几个人一起去买一件物品,如果每人出8元,则多了3元;如果每人出7元,则少了4元钱,问有多少人?该物品价值多少元?
24. 如图,直线 分别与 轴、 轴交于A、B两点.过点B的直线 交 轴于点C.点D 是直线 上的一点,连接CD.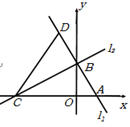 (1)、求AB的长和点D的坐标;(2)、求△BCD的面积.25. 阅读下面的材料:
(1)、求AB的长和点D的坐标;(2)、求△BCD的面积.25. 阅读下面的材料:对于实数 ,我们定义符号 的意义为:当 时, ;当 时, ,如: .
根据上面的材料回答下列问题:
(1)、 ;(2)、当 时,求x的取值范围.26. 已知:如图,AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F.求证:BE=CF.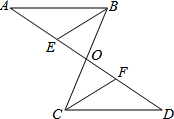 27. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
27. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
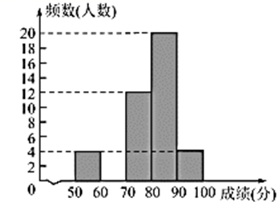
信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息解答下列问题:
(1)、补全第二组频数分布直方图(直接在图中补全);(2)、第三组竞赛成绩的众数是分,抽取的50名学生竞赛成绩的中位数是分;(3)、若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为人.