湘教版初中数学九年级下册4.3用频率估计概率 同步练习
试卷更新日期：2021-12-23 类型：同步测试
一、单选题
-
1. 在抛掷一枚质地均匀的硬币的实验中，第100次抛掷时，反面朝上的概率是（ ）A、 B、 C、 D、不确定2. 一个不透明的袋子里装有黄球18个和红球若干，小明通过多次摸球试验后发现摸到红球的频率稳定在0.4左右，则袋子里有红球（ ）个A、12 B、15 C、18 D、243. 在一个不透明的袋子里，装有6枚白色棋子和若干枚黑色棋子，这些棋子除颜色外都相同．将袋子里的棋子摇匀，随机摸出一枚棋子，记下它的颜色后再放回袋子里．不断重复这一过程，统计发现，摸到白色棋子的频率稳定在0.1，由此估计袋子里黑色棋子的个数为（ ）A、60 B、56 C、54 D、524. 某小组做“用频率估计概率”的实验时，给出的某一结果出现的频率分布折线图，则符合这一结果的实验可能是（ ）
A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、从一个装有2个红球和1个黑球的袋子中任取一球，取到的是黑球 D、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃5. 在一个不透明的袋子中，装有红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同．若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45，则该袋子中的白色球可能有（ ）A、6 个 B、16 个 C、18 个 D、24 个6. 绿豆在相同条件下的发芽试验，结果如下表所示：每批粒数n
100
300
400
600
1000
2000
3000
发芽的粒数m
96
282
382
570
948
1912
2850
发芽的频率
0.960
0.940
0.955
0.950
0.948
0.956
0.950
则绿豆发芽的概率估计值（精确到0.01）是（ ）
A、0.96 B、0.95 C、0.94 D、0.907. 某小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的实验是（ ）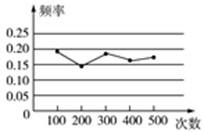
A、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” B、一副去掉大、小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子，向上的面点数是48. 如图，是某射手在相同条件下进行射击训练的结果统计图，该射手击中靶心的概率的估计值为（ ）
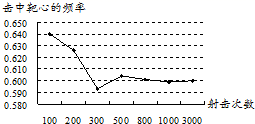A、0.600 B、0.640 C、0.595 D、0.6059. 在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球，除颜色外其它都相同，小明进行了多次摸球实验，发现摸到白色乒乓球的频率稳定在0.2左右，由此可知盒子中黄色乒乓球的个数可能是（ ）A、2个 B、4个 C、18个 D、16个10. 一个不透明的袋子里装有黄、白、红三种颜色的球，摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过多次试验后，发现摸到红球的频率稳定在0.5，则摸到红球的概率约为（ ）A、0.25 B、0.5 C、0.75 D、0.85二、填空题
-
11. 小麦是中国重要的粮食作物之一，传入中国的时间较早据考古发掘新疆孔雀河流域新石器时代遗址出土的炭化小麦，距今400年以上．今年某乡村振兴实验室，从某小麦新品种的种子中抽取6批，在相同条件下进行发芽实验，数据统计如表：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
95
358
744
893
1804
4505
发芽频率
0.950
0.895
0.930
0.893
0.902
0.901
据此可知，该种子发芽的概率为（精确到0.1）．
12. 不透明的箱子里装有大小一样、黑白两种颜色的塑料球共5000个，为了估计两种颜色的球各有多少个，将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后，发现摸到黑球的频率在0.7附近较稳定的波动，据此可以估计箱子里白球个数约是 个．13. 在不透明的袋子里装有颜色不同的16个红球和若干个白球，每次从袋子里摸出1个球，记录下颜色后再放回，经过100次试验，发现摸到白球的次数为60次，估计袋中白球有个．14. 在一个暗箱里放有m个大小相同、质地均匀的白球，为了估计白球的个数，再放入3个同白球大小、质地均相同，只有颜色不同的黄球，每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在25%，推算m的值大约是 ．15. 一个不透明的袋子中有红球和黑球共25个，这些球除颜色外都相同．将袋子中的球搅拌均匀，从中随机摸出一个球，记下它的颜色再放回袋子中．不断重复这一过程，共摸了400次球，发现有240次摸到黑球，由此估计袋中的黑球大约有 个．16. 某商场举办抽奖活动，每张奖券获奖的可能性相同，以10000奖券为一个开奖单位，设特等奖10个，一等奖100个，二等奖500个，则1张奖券中奖的概率是 ．三、解答题
-
17. 4件同型号的产品中，有1件不合格品和3件合格品.在这4件产品中加入 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，由此可以推算出 的值大约是多少？18. 一个口袋中放有16个球，其中红球6个，白球和黑球各若干个，每个球除了颜色外没有任何区别.小明通过大量反复的试验（每次将球搅匀后，任意摸出一个球记下颜色后再放回）发现，取出黑球的频率稳定在 附近，请你估计袋中白球的个数19. 第一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定在0.4，估计袋中红球的个数.
四、综合题
-
20. 王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球试验，每次摸出一个球（有放回），表格是活动进行中的一组统计数据：
摸球的次数
100
150
200
500
800
1000
摸到黑球的次数
23
31
60
130
203
251
摸到黑球的频率
0.23
0.21
0.30
0.26
0.235
0.251
(1)、根据上表数据估计从袋中摸出一个球是黑球的概率是；（精确到 ）(2)、估算袋中白球的个数.21. 在一只不透明的袋子中装有黑球、白球共10个，这些球除颜色外都相同，小明每次摇匀后随机从袋中摸出一个球，记录颜色后放回袋中，通过2000次重复摸球实验后，共摸出黑球1205次．(1)、估计袋中有黑球个；(2)、小明从袋中取出n个黑球后，小明从袋中剩余的球中随机摸出一个球是黑球的概率为 ，求n的值．22. 有一个圆形转盘，分黑色、白色两个区域.(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：实验次数n(次)
10
100
2000
5000
10000
50000
100000
白色区域次数m(次)
3
34
680
1600
3405
16500
33000
落在白色区域频率
0.3
0.34
0.34
0.32
0.34
0.33
0.33
请你利用上述实验，估计转动该转盘指针落在白色区域的概率为
(2)、若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为240°，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.