湘教版初中数学九年级下册4.2概率及其计算 同步练习
试卷更新日期:2021-12-23 类型:同步测试
一、单选题
-
1. 小梅随机选择在下周一至周五的某一天去打新冠疫苗,则她选择在周二去打疫苗的概率为( )A、1 B、 C、 D、2. 有两组扑克牌各三张,牌面数字均为 , , ,随意从每组牌中各抽一张,数字之和等于 的概率是( )A、 B、 C、 D、3. 如图是一个游戏转盘,连续自由转动转盘两次(如果落在分隔线上,则重新转动,直至转到其中一块区域),则两次转动指针都落在数字“Ⅲ”所示区域内的概率是( )
 A、 B、 C、 D、4. 掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率是 ( )A、 B、 C、 D、5. 从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )A、 B、 C、 D、6. 有三张正面分别写有数字﹣2,3,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为点P的横坐标,然后放回再从这三张卡片中随机抽取一张,以其正面的数字作为点P的纵坐标,则点P在第三象限的概率是( )A、 B、 C、 D、7. 一个质地均匀的小正方体,六个面分别标有数字“1”,“2”,“3”“4”,“5”,“6”,抛出小正方体后,观察朝上一面的数字,出现偶数的概率是( )A、 B、 C、 D、8. 在一个不透明的袋子中装有2个黄球和2个红球,它们除颜色外没有其他差别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )A、 B、 C、 D、9. 一个不透明的袋子中有1个红球,1个绿球和 个白球, 这些球除颜外都相同. 从袋中随机摸出一个球, 记录其颜色, 然后放回. 大量重复该实验, 发现摸到绿球的频率稳定于0.25, 则白球的个数 的值可能是 ( )A、1 B、2 C、4 D、510. 如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
A、 B、 C、 D、4. 掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率是 ( )A、 B、 C、 D、5. 从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )A、 B、 C、 D、6. 有三张正面分别写有数字﹣2,3,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为点P的横坐标,然后放回再从这三张卡片中随机抽取一张,以其正面的数字作为点P的纵坐标,则点P在第三象限的概率是( )A、 B、 C、 D、7. 一个质地均匀的小正方体,六个面分别标有数字“1”,“2”,“3”“4”,“5”,“6”,抛出小正方体后,观察朝上一面的数字,出现偶数的概率是( )A、 B、 C、 D、8. 在一个不透明的袋子中装有2个黄球和2个红球,它们除颜色外没有其他差别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是( )A、 B、 C、 D、9. 一个不透明的袋子中有1个红球,1个绿球和 个白球, 这些球除颜外都相同. 从袋中随机摸出一个球, 记录其颜色, 然后放回. 大量重复该实验, 发现摸到绿球的频率稳定于0.25, 则白球的个数 的值可能是 ( )A、1 B、2 C、4 D、510. 如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 有四张大小、形状及背面完全相同的卡片,卡片正面分别画有等边三角形、正方形、平行四边形、菱形,从这四张卡片中任意抽取一张,卡片正面的图形既是轴对称图形又是中心对称图形的概率是 .12. 如图所示,转盘被分成面积相等的8份,小强随机转动转盘一次,则指针指到偶数的概率是 .
 13. 如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
13. 如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 . 14. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .15. 一个布袋里有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出1个球不放回,再摸出1个球,摸出的2个球都是红球的概率是 .16. 如图所示的两个圆盘中,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是 .
14. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .15. 一个布袋里有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出1个球不放回,再摸出1个球,摸出的2个球都是红球的概率是 .16. 如图所示的两个圆盘中,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是 .
三、解答题
-
17. 一只不透明的箱子里共有3个球,其中2个白球.1个红球,它们除颜色外均相同.从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球.请你用列表或画树状图的方法,求两次摸出的球都是白球的概率.18. 小明、小亮和小颖三人做“石头、剪刀和布”的游戏.小颖说:你俩玩,我裁判,并制定了如下的游戏规则:如果你俩的手势相同,我获胜;如果你俩的手势不同,按“石头胜剪刀,剪刀胜布,布胜石头”的规则决定获胜者.假设小明与小亮每次出这三种手势的可能性相同,通过列表或画树状图的方法,分析这个游戏规则是否公平.
 19. 桌面上放有不透明的四张卡片,每张卡片正面都写有一个数字,分别是1,2,3,4,它们除数字外其余全部相同,现将它们背面朝上洗均匀.随机抽取一张卡片,记下数字后放回,洗匀后再随机抽取一张卡片,请用列表或画树状图的方法求出两次数字和为4的概率.
19. 桌面上放有不透明的四张卡片,每张卡片正面都写有一个数字,分别是1,2,3,4,它们除数字外其余全部相同,现将它们背面朝上洗均匀.随机抽取一张卡片,记下数字后放回,洗匀后再随机抽取一张卡片,请用列表或画树状图的方法求出两次数字和为4的概率.四、综合题
-
20. 只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17(1)、从7、11、13、17这4个素数中随机抽取一个,则抽到的数是7的概率是 .(2)、从7、11、13、17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.21. 北京将于2022年举办冬奥会和冬残奥会,中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者,他收集了如下图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好.
 (1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票依次分别用字母A,B,C,D表示)22. 2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
(1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票依次分别用字母A,B,C,D表示)22. 2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.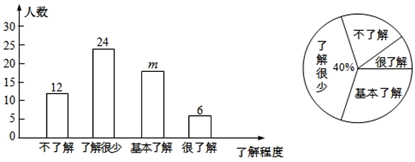
请你根据上面的信息,解答下列问题
(1)、本次共调查了名员工,条形统计图中 ;(2)、若该公司共有员工1000名,请你估计不了解防护措施的人数;(3)、在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.