湘教版初中数学九年级下册3.2直棱柱圆柱的侧面展开图 同步练习
试卷更新日期:2021-12-23 类型:同步测试
一、单选题
-
1. 下列图形中不是正方体的表面展开图的是( )A、
 B、
B、 C、
C、 D、
D、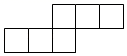
-
2. 如图是某个几何体的展开图,该几何体是( )
 A、三棱柱 B、四棱柱 C、圆柱 D、圆锥
A、三棱柱 B、四棱柱 C、圆柱 D、圆锥 -
3. 如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )
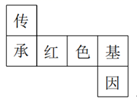 A、传 B、国 C、承 D、基
A、传 B、国 C、承 D、基 -
4. 下列展开图中,不是正方体展开图的是( )A、
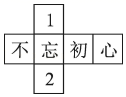 B、
B、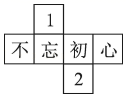 C、
C、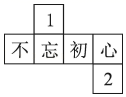 D、
D、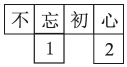
-
5. 下列图形中,可能是圆锥侧面展开图的是( )
 A、
A、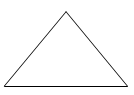 B、
B、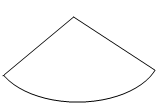 C、
C、 D、
D、
-
6. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
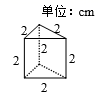 A、
A、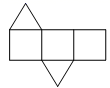 B、
B、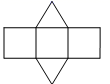 C、
C、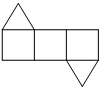 D、
D、
-
7. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
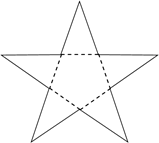 A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱
A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱 -
8. 如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
 A、跟 B、百 C、走 D、年
A、跟 B、百 C、走 D、年 -
9. 下列图形中,不是正方体表面展开图的是( )A、
 B、
B、 C、
C、 D、
D、
-
10. 下图是某个几何体的展开图,该几何体是( )
 A、三棱柱 B、三棱锥 C、圆柱 D、圆锥
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥
二、填空题
-
11. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“融”字一面的相对面上的字是 .

-
12. 下图是某个几何体的展开图,该几何体是 .

-
13. 如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有1个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有种拼接方法.

三、解答题
-
14. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,求x的值.
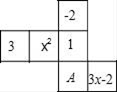
-
15.
有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6,甲、乙、丙三位同学从三个不同的角度去观察此正方体,观察结果如图所示:

请画出正方体的一种表面展开图,(要求把数字标注在表面展开图中)
-
16.
如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.
(1)请把﹣10,8,10,﹣3,﹣8,3分别填入六个小正方形中.
(2)若某相对两个面上的数字分别满足关系式和﹣5,求x的值.

四、综合题
-
17.
一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.
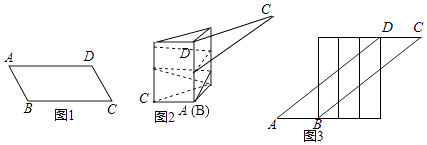 (1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
(1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm. -
18. 阅读下面材料:
实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.

解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,
设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l22=(AB+BC)2=(5+10)2=225.
为比较l1 , l2的大小,我们采用“作差法”:
∵l12﹣l22=25(π2﹣8)>0∴l12>l22∴l1>l2 ,
小明认为应选择路线2较短.
(1)、问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”.请你用上述方法帮小亮比较出l1与l2的大小:
(2)、问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当 满足什么条件时,选择路线2最短?请说明理由.
(3)、问题解决:如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式).
