湘教版初中数学九年级下册2.5.3切线长定理 同步练习
试卷更新日期:2021-12-23 类型:同步测试
一、单选题
-
1. 已知PA , PB是⊙O的切线,A , B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )A、63° B、117° C、53°或127° D、117°或63°2. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
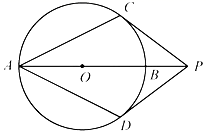 A、 B、 C、 D、3. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为( )
A、 B、 C、 D、3. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为( )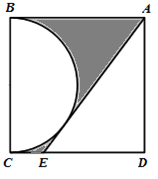 A、 B、 C、1 D、4. 如图,P为⊙O外一点,PA、PB是⊙O 的切线,A , B为切点,点C为AB左侧⊙O上一点,若∠P=50°,则∠ACB的度数为( )
A、 B、 C、1 D、4. 如图,P为⊙O外一点,PA、PB是⊙O 的切线,A , B为切点,点C为AB左侧⊙O上一点,若∠P=50°,则∠ACB的度数为( ) A、50° B、55° C、60° D、65°5. 如图, 、 为 的切线, 、 为切点,点 为弧 上一点,过点 作 的切线分别交 、 于 、 ,若 ,则 的周长等于( ).
A、50° B、55° C、60° D、65°5. 如图, 、 为 的切线, 、 为切点,点 为弧 上一点,过点 作 的切线分别交 、 于 、 ,若 ,则 的周长等于( ).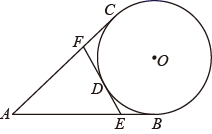 A、6 B、12 C、9 D、186. 如图, 和 是 的两条切线, , 为切点,点 在 上,点 , 分别在线段 和 上,且 , .若 ,则 的度数为( )
A、6 B、12 C、9 D、186. 如图, 和 是 的两条切线, , 为切点,点 在 上,点 , 分别在线段 和 上,且 , .若 ,则 的度数为( )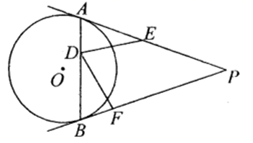 A、 B、 C、 D、7. 如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC , 若∠P=78°,则∠ACB的度数为( )
A、 B、 C、 D、7. 如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC , 若∠P=78°,则∠ACB的度数为( ) A、102° B、51° C、41° D、39°8. 如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是
A、102° B、51° C、41° D、39°8. 如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是 A、 B、 C、 D、9. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( )
A、 B、 C、 D、9. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( ) A、 B、 C、 D、10. 如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么 的值等于( )
A、 B、 C、 D、10. 如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么 的值等于( ) A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
11. 如图,已知 , 分别切⊙O于A、B, 切⊙O于E,若 , ,则△ 周长为.
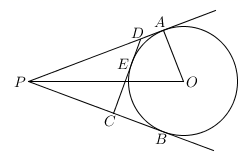 12. 如图,PA、PB是 的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=°.
12. 如图,PA、PB是 的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=°. 13. 如图, , 是 的两条切线, , 为切点,若 , ,则 .
13. 如图, , 是 的两条切线, , 为切点,若 , ,则 .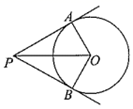 14. 如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为.
14. 如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为. 15. 如图,在 中, ,当半径为1的 在 内自由移动时,圆心 在 内所能到达的区域面积为6,则 的外接圆面积为.
15. 如图,在 中, ,当半径为1的 在 内自由移动时,圆心 在 内所能到达的区域面积为6,则 的外接圆面积为. 16. PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为.
16. PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为.三、解答题
-
17. 如图, , 分别与 相切于 两点,若 ,求 的度数.
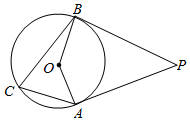 18. 如图, , 分别与⊙O相切于 , 两点,点 在⊙O上,已知 ,求 的度数.
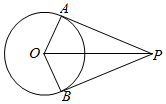
18. 如图, , 分别与⊙O相切于 , 两点,点 在⊙O上,已知 ,求 的度数. 19. 如图,PA , PB是⊙O的切线,A , B为切点,连接OP .
19. 如图,PA , PB是⊙O的切线,A , B为切点,连接OP .求证:OP平分∠AOB .
四、综合题
-
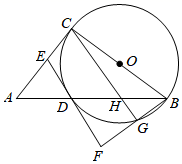
20. 如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB CD,BO=6cm.CO=8cm,
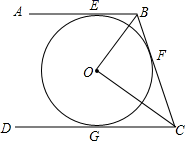 (1)、求证:BO⊥CO;(2)、求⊙O的半径.
(1)、求证:BO⊥CO;(2)、求⊙O的半径.